Rotation

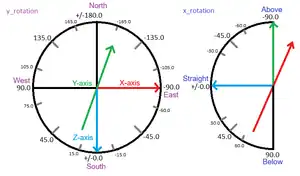
A frog's perspective can be seen as a blue line.

Rotation (also known as perspective, viewpoint or viewing angle) is the direction an entity is facing. Rotation in Minecraft consists of Y-rotation or yaw and X-rotation, declination or pitch, each affecting the directions of the body and the head of the entity. For entities without heads, they can sometimes rotate entirely around the X-axis. The "X" and "Y" refers to the axis about which they rotate. Rotation can limit what a mob or player can see, but other entities (e.g. boats and item frames) also have a rotation.

Representation

Rotation is internally represented with two float values in degrees.

Y-rotation varies from -180° (facing due north) to -90° (facing due east) to 0° (facing due south) to +90° (facing due west) to +180° (facing due north again).
For X-rotation, horizontal is 0°, with positive values looking downward and negative values looking upward. It does not exceed positive or negative 90°.

Debug screen

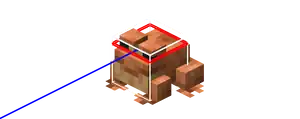
With F3 + B, the rotation of all entities show up as a blue beam.

The player's own rotation can be seen in the debug screen under Facing. First the cardinal direction and axis are mentioned, followed by the two angles for direction and head tilt.

Y-rotation (Yaw Angle)

A change in the Y-rotation angle changes the direction it is facing, to the left or right of its direction of motion.^[1] They are represented in the debug screen correct to 1 decimal place. (The X and Z coordinates are represented correct to 3 decimal places.)

Here, "anticlockwise angle from +X in a 2D system" is thought of as anything in (-180°, 180°], or -180° < x ≤ 180°, where x is one of the angles.

Y-rotation angle ranges based on the cardinal directions
Cardinal Directions	Towards the axis	Y-rotation angle range (ranges inclusive, follows anticlockwise direction)	Range of anticlockwise angle from +X in a 2D system (ranges inclusive, anticlockwise direction)
North	negative Z	-135.1° to 135.1°	45.1° to 134.9°
South	positive Z	45.0° to -44.9°	-135.0° to -45.1°
East	positive X	-45.0° to -135.0°	-45.0° to 45.0°
West	negative X	135.0° to 45.1°	135.0° to -135.1°

Diagram mapping Y-rotation angles to clock positions and cardinal directions, along with the bounding angles (all inclusive) for each cardinal direction. Referred to as a yaw table in this article

Y-rotation angles based on the clock positions
Clock Positions	Y-rotation angle	Anticlockwise angle from +X in a 2D system
1 o'clock	-150.0°	60.0°
2 o'clock	-120.0°	30.0°
3 o'clock	-90.0°	0.0°
4 o'clock	-60.0°	-30.0°
5 o'clock	-30.0°	-60.0°
6 o'clock	-0.0°	-90.0°
7 o'clock	30.0°	-120.0°
8 o'clock	60.0°	-150.0°
9 o'clock	90.0°	180.0°
10 o'clock	120.0°	150.0°
11 o'clock	150.0°	120.0°
12 o'clock	180.0°	90.0°

Algorithm for the Y-rotation angle

Explanation

The angle transformation to get the correct Y-rotation angle will not only require rotating the Y-rotation circle, but also reflecting the yaw table horizontally or vertically through the diameter.

Initial and Desired

A semicircle in Minecraft, placed in a valley using spruce logs and jungle place. Orientation is like a dome. — This is the upper half of a normal circle with the actual angles written. Compare this picture to the one given above. We want to get the angles written as the Y-rotation angle.

Think of this part as the top half of a semicircle standing on the +X axis. It will be rotated for getting the outputs as in the yaw table (and we will check if we need to flip).

A semicircle in Minecraft, placed in a valley using spruce logs and jungle planks. Orientation is towards the left. Mirror of the "Semicircle rotated by minus 90 degrees" image. — The desired angles we want. The 180 degree part is above the 0 degree part, and the semicircle is in a C-like orientation.

What we want
Initial angle (+X axis, anticlockwise)	Desired angle (Corresponding Y-rotation angle)	Orientation	Desired position in the semicircle
0°	-90°	Towards the left	Bottom
90°	180°		Left
180°	90°		Top

Semicircle rotated by plus 90 degrees, orientation of the semicircle is towards the left. — Semicircle rotated by +90°.

Adding 90°


Initial angle (+X axis, anticlockwise)	Final angle (Corresponding Y-rotation angle)	Orientation	Final position in the semicircle
0°	90°	Towards the left	Top
90°	180°		Left
180°	-90°		Bottom

Reflecting the semicircle along the (imaginary) horizontal diameter will produce the desired angles (Top will be changed to bottom and vice-versa).

Semicircle rotated by minus 90 degrees, orientation of the semicircle is towards the right. — Semicircle rotated by -90°.

Subtracting 90°


Initial angle (+X axis, anticlockwise)	Final angle (Corresponding Y-rotation angle)	Orientation	Final position in the semicircle
0°	-90°	Towards the right	Bottom
90°	0°		Right
180°	90°		Top

Reflecting the semicircle along the vertical diameter will produce the desired angles (Right will be changed to left and vice-versa).

Wrapping back

For the yaw, the range is (-180°, 180°], which means that anything greater than the absolute value of 180 degrees must be wrapped back inside the yaw table. However, after the angle transformations, all the angles beyond the range will have to be wrapped.

There can be many more approaches for wrapping other than the ones stated below.

Approach 1: Using the modulus

Required: the size and the minimum and the maximum values.

The size is 360° because the whole circle is being considered.

Therefore,

$\begin{aligned} - 190 \equiv 170 (\mod 360) \\ 181 \equiv - 179 (\mod 360) \end{aligned}$

In various programming languages, the mod(a, n) operator is used. When exactly one of the operands is negative, the basic definition breaks down, and programming languages differ in how these values are defined.^[2] Here, n = 360. Therefore, 'a' should be changed to a positive value before performing the modulo operation.

Approach 2: Adding or subtracting by 90 degrees in certain quadrants

Place blocks

The viewing angle affects the placement of some blocks: depending on how the player look, for example, a banner or a sign rotated accordingly. The viewing angle also plays a role when placing stairs or scaffolding.

Target selection

Target selection properties allow entities to be selected that have a specific viewing angle:

y_rotation	Viewing angle
x_rotation	Head tilt angle

Angle ranges are specified with two points, e.g. B. 43..47.

/title @a[y_rotation=<view angle>] actionbar {"text":"View direction (compass direction)"}

/title @a[x_rotation=<head tilt angle>] actionbar {"text":"head tilt (up)"}

Examples of the cardinal directions:

/execute if entity @p[y_rotation=135..-135] run say North
/execute if entity @p[y_rotation=-135..-45] run say East
/execute if entity @p[y_rotation=-45..45] run say South
/execute if entity @p[y_rotation=45..135] run say West

Save perspective

Blinking angles can be read out and saved in a score: To do this, create a score target for the direction and the inclination.

/scoreboard objectives add direction dummy "viewing angle direction" 
/scoreboard objectives add inclination dummy "viewing angle inclination"

Then, read out the direction and inclination using the command /data and save them in the respective score.

/execute as @a store result score @s direction run data get entity @s Rotation[0]
/execute as @a store result score @s tilt run data get entity @s Rotation[1]

Set perspective

The commands /teleport and /rotate can be used to set the perspective of entities. The entities can move freely after teleportation if they have AI, but they start with the fixed viewing angle.

Additionally, all entities except players can be realigned using the command /data via the property Rotation

Viewpoint coordinates

Circumflexes (^) allow the position to be determined depending on the rotation of an entity.

History

This section of the article is empty.

You can help by expanding it.

Navigation

[1] ttps://en.wikipedia.org/wiki/Yaw_(rotation)

[2] ttps://en.wikipedia.org/wiki/Modulo

[1]

[2]

v t e Gameplay
General mechanics	Add-ons Attribute Commands Distance Effect Potency Explosion Game rules Interaction range Inventory Creative inventory Saved Hotbars Generated loot Hitbox Multiplayer Server Server list Realms Splitscreen Oxidation Rarity Legacy Redstone circuits Conductivity Renewability Renewable Non-renewable Snowlogging South-east rule Spawn protection Tiers Waterlogging
Survival	Achievements Advancements Archaeology Armor materials Bartering Breaking Instant mining Breeding Brewing Cooking Crafting 2×2 grid Recipe book Dual wield Difficulty Durability Enchanting Experience Farming Fishing Health Healing Hunger Item repair Mob spawning Ominous Event Ominous Trial Raid Patrol Raid captain Smelting Smithing World Spawn Taming Trading Workstations Zombie siege
Combat	Blocking Damage Attack cooldown Critical hit Knockback Sprint-knockback Drops Monster infighting Geared mobs
Environment	Biomes Daylight cycle Dimensions Seeds Structures Weather World generation More
Movement	Crawling Flying Gliding Jumping Lying Riding Sitting Sneaking Sprinting Swimming Walking
User interface	Action bar Bossbar Chat Death messages Game mode switcher Heads-up display Narrator Locator bar Scoreboard Toasts Tutorial hints Tooltip
Visuals	Color Block colors Item colors Effect colors Miscellaneous colors Emotes Enchantment glint Error Light Resource pack Screen effects Skins Character Skin pack Third-person view Vibrant Visuals
Outdated	Sword blocking Materials Update Suppression