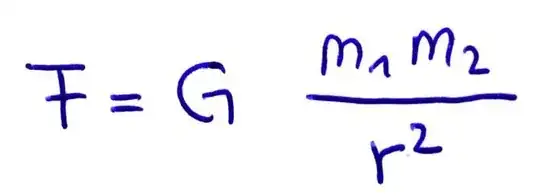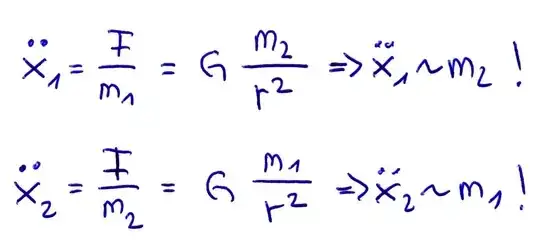Don't heavier objects actually fall faster because they exert their own gravity?

Question

The common understanding is that, setting air resistance aside, all objects dropped to Earth fall at the same rate. This is often demonstrated through the thought experiment of cutting a large object in half—the halves clearly don't fall more slowly just from having been sliced into two pieces.

However, I believe the answer is that when two objects fall together, attached or not, they do "fall" faster than an object of less mass alone does. This is because not only does the Earth accelerate the objects toward itself, but the objects also accelerate the Earth toward themselves. Considering the formula: $$ F_{\text{g}} = \frac{G m_1 m_2}{d^2} $$

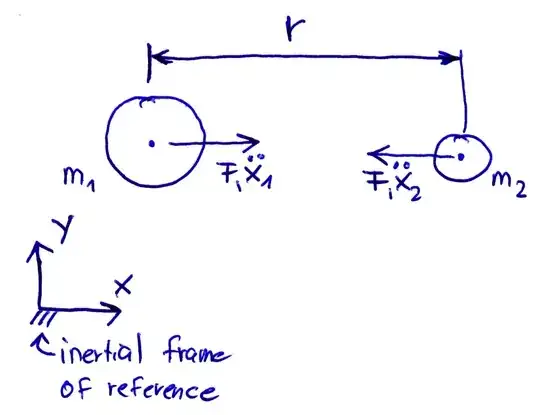
Given $F = ma$ thus $a = F/m$, we might note that the mass of the small object doesn't seem to matter because when calculating acceleration, the force is divided by $m$, the object's mass. However, this overlooks that a force is actually applied to both objects, not just to the smaller one. An acceleration on the second, larger object is found by dividing $F$, in turn, by the larger object's mass. The two objects' acceleration vectors are exactly opposite, so closing acceleration is the sum of the two:

$$ a_{\text{closing}} = \frac{F}{m_1} + \frac{F}{m_2} $$

Since the Earth is extremely massive compared to everyday objects, the acceleration imparted on the object by the Earth will radically dominate the equation. As the Earth is $\sim 5.972 \times {10}^{24} \, \mathrm{kg} ,$ a falling object of $5.972 \times {10}^{1} \, \mathrm{kg}$ (a little over 13 pounds) would accelerate the Earth about $\frac{1}{{10}^{24}}$ as much, which is one part in a trillion trillion.

Thus, in everyday situations we can for all practical purposes treat all objects as falling at the same rate because this difference is so small that our instruments probably couldn't even detect it. But I'm hoping not for a discussion of practicality or what's measurable or observable, but of what we think is actually happening.

Am I right or wrong?

What really clinched this for me was considering dropping a small Moon-massed object close to the Earth and dropping a small Earth-massed object close to the Moon. This thought experiment made me realize that falling isn't one object moving toward some fixed frame of reference, and treating the Earth as just another object, "falling" consists of multiple objects mutually attracting in space.

Clarification: one answer points out that serially lifting and dropping two objects on Earth comes with the fact that during each trial, the other object adds to the Earth's mass. Dropping a bowling ball (while a feather waits on the surface), then dropping the feather afterward (while the bowling ball stays on the surface), changes the Earth's mass between the two experiments. My question should thus be considered from the perspective of the Earth's mass remaining constant between the two trials (such as by removing each of the objects from the universe, or to an extremely great distance, while the other is being dropped).

Answer 1

Using your definition of "falling," heavier objects do fall faster, and here's one way to justify it: consider the situation in the frame of reference of the center of mass of the two-body system (CM of the Earth and whatever you're dropping on it, for example). Each object exerts a force on the other of

$$F = \frac{G m_1 m_2}{r^2}$$

where $r = x_2 - x_1$ (assuming $x_2 > x_1$) is the separation distance. So for object 1, you have

$$\frac{G m_1 m_2}{r^2} = m_1\ddot{x}_1$$

and for object 2,

$$\frac{G m_1 m_2}{r^2} = -m_2\ddot{x}_2$$

Since object 2 is to the right, it gets pulled to the left, in the negative direction. Canceling common factors and adding these up, you get

$$\frac{G(m_1 + m_2)}{r^2} = -\ddot{r}$$

So it's clear that when the total mass is larger, the magnitude of the acceleration is larger, meaning that it will take less time for the objects to come together. If you want to see this mathematically, multiply both sides of the equation by $\dot{r}\mathrm{d}t$ to get

$$\frac{G(m_1 + m_2)}{r^2}\mathrm{d}r = -\dot{r}\mathrm{d}\dot{r}$$

and integrate,

$$G(m_1 + m_2)\left(\frac{1}{r} - \frac{1}{r_i}\right) = \frac{\dot{r}^2 - \dot{r}_i^2}{2}$$

Assuming $\dot{r}_i = 0$ (the objects start from relative rest), you can rearrange this to

$$\sqrt{2G(m_1 + m_2)}\ \mathrm{d}t = -\sqrt{\frac{r_i r}{r_i - r}}\mathrm{d}r$$

where I've chosen the negative square root because $\dot{r} < 0$, and integrate it again to find

$$t = \frac{1}{\sqrt{2G(m_1 + m_2)}}\biggl(\sqrt{r_i r_f(r_i - r_f)} + r_i^{3/2}\cos^{-1}\sqrt{\frac{r_f}{r_i}}\biggr)$$

where $r_f$ is the final center-to-center separation distance. Notice that $t$ is inversely proportional to the total mass, so larger mass translates into a lower collision time.

In the case of something like the Earth and a bowling ball, one of the masses is much larger, $m_1 \gg m_2$. So you can approximate the mass dependence of $t$ using a Taylor series,

$$\frac{1}{\sqrt{2G(m_1 + m_2)}} = \frac{1}{\sqrt{2Gm_1}}\biggl(1 - \frac{1}{2}\frac{m_2}{m_1} + \cdots\biggr)$$

The leading term is completely independent of $m_2$ (mass of the bowling ball or whatever), and this is why we can say, to a leading order approximation, that all objects fall at the same rate on the Earth's surface. For typical objects that might be dropped, the first correction term has a magnitude of a few kilograms divided by the mass of the Earth, which works out to $10^{-24}$. So the inaccuracy introduced by ignoring the motion of the Earth is roughly one part in a trillion trillion, far beyond the sensitivity of any measuring device that exists (or can even be imagined) today.

Answer 2

In addition to the already given answears this also might be of interest:

When hammer and feather are dropped simultaneously they arrive at the same time, when dropped independently the hammer attracts the planet more than the feather, so you are right, the total time until impact is then smaller for the hammer.

If you pick up the hammer and let it fall to the ground while the feather lies on the ground and its mass adds to the planet's mass (neglecting desity inhomogeneities) it takes the same time as when you pick up the feather and let it fall down while the hammer is on the ground and its mass adds to the planet, since m1+m2+m3=constant.

When you drop hammer and feather simultaneously, the feather will travel the longer distance in the same time, and is therefore faster than the hammer, since the planet is moving more towards the hammer than to the feather, and the feather is attracted by the largest sum of masses.

The initial distance of the point masses is 1 meter; in the first example you have 1000kg vs 100kg vs 1kg and in the second one 1000kg vs 666.̇6kg vs 500kg. As you can see the "hammer" and the "feather" arrive at the same time:

---

Answer 3

Inertial Reference Frames

The paradox appears because the "rest frame" of the Earth is not an inertial reference frame, it is accelerating. Keep yourself in the CM (center of mass) reference frame and, at least for two bodies, there is no paradox. Given an Earth of mass $M$, a body of mass $m_i$ will fall towards the center of mass $x_\textrm{CM}=(M x_M + m_i x_i)/(M+m_i)$ with an acceleration $GM/(x_i-x_M)^2$. Note that $\ddot x_\textrm{CM}=0$

Really we have only hidden the paradox, because of course $x_\textrm{CM}$ is different for each $m_i$. But this is a first step to formulate the problem in a decent inertial frame.

The Paradox Resurfaces

The paradox resurfaces again if you want to get rid of $(x_i-x_M)$. In most applications, now that you are in a non-accelerating reference system, you want to consider distances related to it, i.e., $x_i-X_\textrm{CM}$. The solution is to redefine the mass. As $x_i-x_\textrm{CM} = M (x_i - x_M) /(M+m_i)$, we can say that the object $i$ falls into the Mass Center with an acceleration $G{M^3 \over (M+m_ i)^2}{1 \over (x_i-x_\textrm{CM})^2}$ You could say that the actual mass of the "earth at center of mass" is this correction.

Reduced Mass of the System

Once you are into the trick of changing the value of the mass, you can still stick to the reference frame of the earth. In this reference frame the quotient between force and acceleration is $Mm_i/M+m_i$. You can claim that this is the actual mass of the body during the calculation. This is called the reduced mass $m_r$ of the system, and you can see that for small $m_i$, it is almost equal to $m_i$ itself. You can even write some of the previous formulae using the reduced mass $m_r$ in combination with the original masses, for instance the above ${M^3 \over (M+m_ i)^2} = M {m_r^2\over m^2}$, but I am not sure of how useful it is. In any case, you see that you were right about the "heavier implies faster" but that it is perfectly managed.

Three Objects

For three objects, $m_1$ and $m_2$ falling into $M$, the question is how to compare the case to $m_1+m_2$ falling into $M$. You separate the forces between internal, between 1 and 2, and external, against $M$. Look at the point $x_0= {m_1 x_1 + m_2 x_2 \over m_1+m_2}$ . This point is not accelerated by the internal forces. And the external forces move them as $$\ddot x_0={1 \over m_1+m_2} \left(m_1 {G M \over (x_1-x_M)^2} + m_2 {G M \over (x_2-x_M)^2}\right)={F_1+F_2 \over m_1 + m_2}$$ .

The TLDR Answer

This is becoming long...

¡I can not put all the Principia in a single answer!

So you can forget all the previous stuff, considering that just a means to fix notation and get some practice, and read the answer:

If the two bodies are at the same distance $x$ from the "external" earth, they suffer the same external acceleration $g=GM/(x-x_M)^2$, and the same happens with $x_0$. If both bodies are in an approximation where $g$ can be considered constant, which was the case originally considered by Galileo (and the modern $g=9.8~{\rm m/s^2}$), then they have the same acceleration—and also the combined position $x_0$. If they are not at the same distance nor in an approximation of a constant equal-everywhere field, then you can still save the movement of $x_0$ to work as if it were a gravitational force for some single mass $m_T$, but then the manipulation of the equations will produce in the relative positions of $x_1$ and $x_2$ some accelerations of the order of $1/(x_0-x_M)^3$. Such forces are the "tidal forces".

Answer 4

The answer is yes: in principle there is such an effect. When the mass of the dropped object is small compared to the mass of the planet, the effect is very small, of course, but in principle it's there.

Answer 5

I agree. My understanding is the same as well.

Assuming that the earth, mars and moon are of the same size - If the earth and mars where to be suspended in space (mars falling on earth), they would come into contact faster than - if earth and moon were to be suspended in space (moon falling on earth) owing to the fact that mars would cause the earth to accelerate towards it more than moon. This is provided that the distance between the two objects are the same initially. The earth would attract both at the same rate for any given distance.

I have also posted here regarding what would fall first in case of three objects being involved, asking if my understanding is correct. It is the classic apple-feather experiment revisited. I hope it clarifies @KeithThompson 's question above.

Answer 6

Disclaimer

I am not a physicist, I am "just" an engineer.

Not sure if that counts as an answer but at least I use some scribbles :).

I would depict the (one dimensional) situation as this:

• There are two objects $m_1$ and $m_2$ with mass. The dot in the middle is the center of mass for each object.
• The distance between the centers of mass is denoted as $r$.
• There is also a frame of reference which is not accelerated at all (a so-called inertial frame of reference).
• The two masses are attracted to each other by the force $F$ which is described by Newton's law of universal gravitation.

The absolute acceleration of each object $\ddot{x}_1$ and $\ddot{x}_2$ can be formulated as:

• $\ddot{x}_1$ and $\ddot{x}_2$ are measured against the inertial frame of reference.
• The acceleration is proportional ($\sim$) to the mass of the opposite index ($1\to2$ and $2\to1$).
• The closing acceleration $a_{closing}$ (or approaching-each-other acceration) however is proportional to the sum of $m_1$ and $m_2$.

Answer 7

Yes, a heavy object dropped from the same height will fall faster then a lighter one. This is true in the rest frame of either object. You can see this from $F=GmM/r^2=m\cdot a=m\cdot d^2r/dt^2$.

The fastest "falling" (since we are re-defining falling) object however is a photon, which has no mass.

Answer 8

The free fall time of two point masses is $ t = \frac{\pi}{2} \sqrt{ \frac{r^3}{2 G(m1+m2)}} $.

The free fall time is dependent on the sum of the two masses. For a given total mass, the free fall time is independent of the ratio of the two masses. The free fall time is the same whether m₁ = m₂, or m₁ >> m₂.

When a body is picked up to a certain height and then dropped, the time to fall to the Earth does not depend on the mass of the object. If you lift a ping-pong ball and then drop it, it will take the same time to fall to the Earth as a bowling ball. Splitting the Earth into two masses does not change the sum of those masses, or the free fall time.

However, when an external body is brought to a certain height above the Earth and then dropped, the free fall time does depend on the mass of the external body. Because the sum of the Earth and the external body obviously does depend on the mass of the external body.

"Most bodies fall at the same rate on earth, relative to the earth, because the earth's mass M is extremely large compared with the mass m of most falling bodies. The body and the earth each fall toward their common center of mass, which for most cases is approximately the same as relative to the earth. In principle, the results of a free fall experiment depend on whether falling masses originate on earth, are extraterrestrial, are sequential or concurrent, or are simultaneous for coincident or separated bodies, etc. When falling bodies originate from the earth, all bodies fall at the same rate relative to the earth because the sum m + M remains constant.
-- ArXiv:Deterrents to a Theory of Quantum Gravity

Assumptions:
The Earth is isolated (there is no moon, sun, etc).
The Earth is non-rotating.
The Earth has no atmosphere. (A hot air balloon would fall upwards because it is less dense than the atmosphere it displaces.)

Answer 9

Drop a 5 lb iron barbell and a 25 lb iron barbell simultaneously. The'll hit the ground simultaneously. The only possible caveat is the recoil effect Ted Bunn brings up above.

Answer 10

Let's keep it simple. Opening my textbook from 1964, "Physics, 4th ed", Hausmann & Slack, Nostrum Co., NY, 1957. When we are contemplating the laws of everyday objects in free fall near the surface of the earth (our only frame of reference), all other forces removed or neutralized, we are in the realm of Newtonian Physics.

F = G(Mm)/r^2; where G is the gravitational constant, M is the mass of the earth, m is the mass of our object, and r is the radius of the earth.

By definition, when at rest on the surface of the earth, the weight ,W, of the object is the repulsive force in the equation F = ma, and a = g, the acceleration due to gravity. Therefore, W = mg, and g = W/m. Substituting into our general gravity equation between two object, we have:

W = G(Mm)/r^2, thus W/m = GM/r^2

Therefore, W/m is a constant! Thus an object will fall with the same acceleration regardless of mass near the surface of the earth.

Had me worried there for a moment :)

Answer 11

A simple explanation is that it takes more FORCE to ACCELERATE an object of greater MASS. A=F/M....or with a constant FORCE, the ACCELERATION is inversely proportional to the MASS. The is a result of inertia.

A larger mass dropped (on a massive objects) requires a GREATER force to accelerate; additionally a GREATER mass exerts a GREATER gravitaional force.

Setting newtons second law to the gravitional force law cancles mass out and therefore renders MASS not related to the ACCELERATION of two gravitationally related objects.