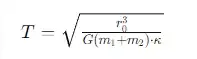Do objects really "fall" at the same rate?

Question

I understand that a hammer and a feather were dropped on the moon and they both landed at the same time. I understand that for all practical intents and purposes all objects do fall at the same rate.

But I don't think they actually do. Because what I think people are forgetting is that the falling object also pulls on the planet/moon.

Given the following masses:

a=9
b=0.2
c=0.1

and the formula for the time it takes for two masses to collide under the mutual gravitational collapses:

it works out that a and b will touch faster than a and c. Am I missing something? I know the effect is so small that in the real world it can be neglected.

Answer 1

You are right in that if you release from some height objects of different masses at different times, the acceleration relative to the surface (which moves with the planet) will depend on the mass of the object too, at a small correction (actually $a_1=-G(M+m_1)/R^2$. However, if you release both object at the same time, they will both accelerate at the same rate relative to the center of the planet.

Answer 2

The effect you cite is so tiny as to be unmeasurable. This is why in most such calculations it is neglected with no loss in accuracy.