What are the different approaches to determine the equivalent resistance of nontrivial resistor networks in general, that cannot be reduced by the usual series and parallel rules? (The diagram below is just one the simplest examples of such a circuit.)
I'll give the answer to this question using an unusual method that showed up in the American Mathematical Monthly's problem section perhaps in the late 1970s. This is not necessarily the easy way to solve the problem, but it works out nicely from an algebraic point of view.
The way most people solve most resistance problems is to use series and parallel resistor rules. These are mathematically elegant in that they involve only resistance. But this circuit cannot be reduced to series and parallel rules (is this true if you write an infinite series in R3, perhaps?), so probably the most straightforward method is to apply a voltage of V to the circuit and use algebra to work out the total current. This is inelegant (but physical) in that it introduces ideas other than resistance itself.
The "delta" method mentioned by Manishearth, (but at this time not actually worked out to the final answer) is how an EE would solve the problem. It has the advantage of sticking with resistance, but it involves somewhat unintuitive changes to the topology of the circuit.
The method I'm giving here uses only resistances and illustrates a general solution to this sort of problem. If one generalizes the $R_k$ to complex numbers $Z_k$, it can be used for general impedances (as can the delta method), but it is more general than the delta method. It also may help with student's understanding of sheet resistance so I think it's worth my time to type it in:
First, we replace the resistors with thin flat material that happens to have a "sheet resistance" of 1 ohm per square. With such a material, if we cut out a rectangle of dimensions 1 x R, we will obtain a resistance of R ohms between two conductors attached to the 1 length sides:
Now the thing about sheet resistance is that you can scale the resistor to whatever size you like; so long as you keep the ratio of the side lengths as "R", the resulting resistor will have resistance R. The sheet can be made up of little sheets that are pasted together. To do the pasting correctly, we need to use insulating glue for the horizontal connections and conducting glue for the vertical connections. This is because current only flows from left to right. So the insulating glue doesn't help or hinder the current flow, and the vertical connections don't matter because all the conducting glue has the same voltage anyway. I saw this method of computing resistors in a solution to problem E2459 at the American Mathematical Monthly, February 1975.
So replace the given circuit with one where each resistor is replaced by a rectangular region with dimensions appropriate for its resistance. In doing this, we have to make an assumption about which way current flows through resistor R3. I'll assume it flows from top to bottom. And in order to set a scale for the whole thing, let's make the vertical dimension of R3 to be length 1. This gives us the following drawing:
Now the overall circuit has a resistance given by the ratio of its length to its width:
$$R = L/W = (R_1 x_1 + R_2x_2)/(x_1+x_4)$$
There are four unknowns, $\{x_1,x_2,x_4,x_5\}$. Comparing horizontal dimensions gives two independent equations:
$$R_1x_1 = R_4x_4 + R_3,$$
$$R_5x_5 = R_3 + R_2x_2.$$
And comparing vertical dimensions gives:
$$x_1 = 1 + x_2,$$
$$x_5 = 1 + x_4.$$
This eliminates $x_1$ and $x_5$ to give two independent equations in two unknowns:
$$R_1 + R_1x_2 = R_4x_4 + R_3,$$
$$R_5 + R_5x_4 = R_3 + R_2x_2.$$
Or:
$$ R_1x_2 - R_4x_4 = R_3-R_1,$$
$$-R_2x_2+ R_5x_4 = R_3-R_5 .$$
These solve to give:
$$ x_2 = \frac{R_3R_5-R_1R_5 + R_3R_4-R_4R_5}{R_1R_5-R_2R_4},$$
$$ x_4 = \frac{R_1R_3-R_1R_5 + R_2R_3-R_1R_2}{R_1R_5-R_2R_4},$$
and so
$$ x_1 = \frac{R_3R_5-R_2R_4 + R_3R_4-R_4R_5}{R_1R_5-R_2R_4},$$
$$ x_5 = \frac{R_1R_3-R_2R_4 + R_2R_3-R_1R_2}{R_1R_5-R_2R_4},$$
We need $W=x_1+x_4:$
$$W = \frac{R_3(R_1+R_2+R_4+R_5)-(R_1+R_4)(R_2+R_5)}{R_1R_5-R_2R_4}$$
and $L = R_1x_1+R_2x_2:$
$$L = \frac{R_3(R_4+R_5)(R_1+R_2)-R_1R_2(R_4+R_5)-R_4R_5(R_1+R_2)}{R_1R_5-R_2R_4}$$
so the total resistance is:
$$R = L/W = \frac{R_1R_4(R_2+R_5)+R_2R_5(R_1+R_4)-R_3(R_4+R_5)(R_1+R_2)}{(R_2+R_5)(R_1+R_4)-R_3((R_1+R_2)+(R_4+R_5))}.$$
In the above, I've grouped terms in order to make it clear that this gives the correct answer in the limit of $R_3$ goes to $0$ or $\infty$.
Use a star-delta transform to simplify part of the circuit. You may also use the principle of superposition.
A x----x-----[1]-----x-----[2]-----x----x B
| | |
[4] [3] [5]
| | |
|-------------x-------------|
$\uparrow$ Fig.1. OP's original circuit.
As suggested by Manishearth, one can perform a $Y$-$\Delta$ transform from $Y$-resistances $R_1$, $R_2$ and $R_3$, to $\Delta$-resistances $R_{12}$, $R_{23}$ and $R_{31}$ (using a $123$ symmetric labeling convention), cf. Fig.2 below.
A x----x------x----[12] ----x------x----x B
| | | |
[4] [31] [23] [5]
| | | |
|------x-------------x------|
$\uparrow$ Fig.2. A $\Delta$-equivalent circuit to OP's original circuit.
In terms of formulas, the $Y$-$\Delta$ transform is$^1$ $$ R_{ij}~=~R_{ji}~=~R_iR_j\sum\limits_{\ell=1}^3R_{\ell}^{-1},\qquad i,j~\in~\{1,2,3\},\qquad i~\neq~j, \tag{1}\label{eq:1}$$ and the $\Delta$-$Y$ transform is$^2$ $$R_k~=~\frac{R_{k,k+1}R_{k-1,k}}{\sum\limits_{\ell=1}^3R_{\ell,\ell+1}}, \qquad k~\in~\mathbb{Z}/3\mathbb{Z}. \tag{2}\label{eq:2}$$
The $\Delta$-equivalent circuit in Fig.2 can be viewed as composed of only series and parallel resistors. The equivalent conductance between $A$ and $B$ therefore becomes
$$ \frac{1}{R}~=~\frac{1}{R_{12}}+\frac{1}{\dfrac{1}{\dfrac{1}{R_{31}}+\dfrac{1}{R_4}} +\dfrac{1}{\dfrac{1}{R_{23}}+\dfrac{1}{R_5}}}, \tag{3}$$ which answers OP's question.
(Finally, let us mention that it is also possible to apply the $Y$-$\Delta$ transform to other triples of the five resistors than $123$.)
$^1$Sketched proof of eq. $\eqref{eq:1}$ via short-cutting nodes $j$ and $k$. Let $i,j,k$ be different. Define $$ S_{jk}~:=~R_{ij}^{-1}+R_{ik}^{-1}~=~\left(R_i+\frac{R_jR_k}{R_j+R_k}\right)^{-1}~=~\frac{R_j+R_k}{\sum\limits_{\ell=1}^3R_{\ell}R_{\ell+1}}\tag{4}\label{eq:4}$$ $$\quad\Downarrow\quad$$ $$R_{ij}^{-1}~\stackrel{\eqref{eq:4}}{=}~\frac{S_{ik}+S_{jk}-S_{ij}}{2}~\stackrel{\eqref{eq:4}}{=}~\frac{R_k}{\sum\limits_{\ell=1}^3R_{\ell}R_{\ell+1}}.\tag{5}$$ $\Box$
$^2$Sketched proof of eq. $\eqref{eq:2}$ via not connected/free node $k$. Let $i,j,k$ be different. Define $$ S_{ij}~:=~R_i+R_j~=~\left(R_{ij}^{-1}+\frac{1}{R_{ik}+R_{jk}}\right)^{-1}~=~\frac{R_{ij}R_{ik}+R_{ij}R_{jk}}{\sum\limits_{\ell=1}^3R_{\ell,\ell+1}}\tag{6}\label{eq:6}$$ $$\quad\Downarrow\quad$$ $$R_k~\stackrel{\eqref{eq:6}}{=}~\frac{S_{ik}+S_{jk}-S_{ij}}{2}~\stackrel{\eqref{eq:6}}{=}~\frac{R_{ik}R_{jk}}{\sum\limits_{\ell=1}^3R_{\ell,\ell+1}}.\tag{7}$$ $\Box$
Here is how I would do it, following the method outlined by kleingordon in a comment. This method is less cool but more general than Carl Brannen's answer, because it will work even in the case where there are crossing wires and you can't rearrange it into a single sheet of resistive material.
Let the electric potential at $A$ be $V_A$ and that at $B$ be $V_B$. Also, let the potential on the wire that connects $R_1$ to $R_2$ and $R_3$ be $V_C$ and let the potential on the wire connecting $R_4$ to $R_3$ and $R_5$ be $V_D$. We know that the current across each resistor must equal the potential difference divided by the resistance, so we have $$I_1 = R_1(V_A - V_C)$$ $$I_2 = R_2(V_C - V_B)$$ $$I_3 = R_3(V_C - V_D)$$ $$I_4 = R_4(V_A - V_D)$$ $$I_5 = R_5(V_D - V_B).$$
We also know that the current must be conserved at every junction, which gives us $$ I_1 + I_2 = I_4 + I_5 $$ $$ I_1 = I_2 + I_3 $$ $$ I_4 + I_3 = I_5, $$ but the last of these three equations is redundant because it can be derived from the other two, so there are seven equations in total, in nine unknowns (five currents and four potentials).
We want to calculate the resistance, which is given by $(V_A-V_B)/(I_1+I_2).$ Since everything's linear we can assume without loss of generality that $V_B=0$ and $V_A=1$. This gives us seven equations in seven unknowns, which we can solve to find the answer.
I haven't worked it through because it's a bit laborious (I'd probably use a computer algebra system rather than doing it by hand) but it should give the same answer as Carl Brannen's method.
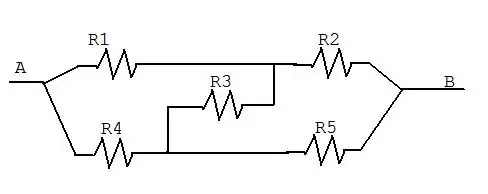
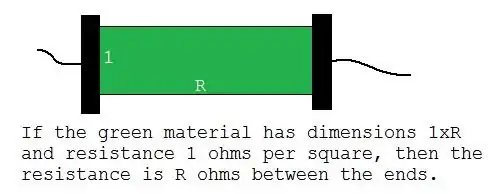
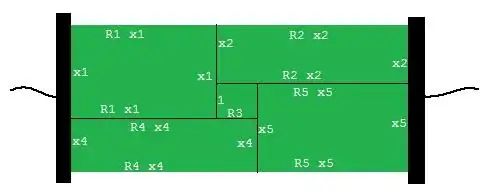
Following on from A Googler's comment to Carl Brannen's answer:
But I think $R_1x_1=R_4x_4−R_3$ and $R_5x_5=R_2x_2−R_3.$ What I'm doing wrong? Please explain
If you follow this correction through, (ie. swap your subscript 1's and 4's, and 2's and 5's in your opening horizontal consideration - the vertical statements do not need changing), then you achieve a similar result to:
$$ R = L/W = \frac{R_1R_4(R_2+R_5)+R_2R_5(R_1+R_4)-R_3(R_4+R_5)(R_1+R_2)}{(R_2+R_5)(R_1+R_4)-R_3((R_1+R_2)+(R_4+R_5))}. $$
but without the negative signs of each $R_3$ term:
$$ R = L/W = \frac{R_1R_4(R_2+R_5)+R_2R_5(R_1+R_4)+R_3(R_4+R_5)(R_1+R_2)}{(R_2+R_5)(R_1+R_4)+R_3((R_1+R_2)+(R_4+R_5))}. $$
This result also gives the correct results for both R tending to 0 and also R tending to infinity, but the definitions of the R's are now consistent with the diagram.
Here are some steps:
We have:
$$ R_1x_1 = R_4x_4 - R_3, $$
$$ R_5x_5 = R_2x_2 - R_3. $$
Using also:
$$ x_1 = x_2 + 1, $$
$$ x_5 = x_4 + 1, $$
and eliminating $x_1$ and $x_5$ from the horizontal equations, we get:
$$ R_1x_2 + R_1 = R_4x_4 - R_3, $$
$$ R_2x_2 - R_3 = R_5x_4 + R_5. $$
These solve to give:
$$x_4 = \frac{R_1R_5 + R_1R_3 + R_1R_2 + R_2R_3}{R_2R_4 - R_1R_5} $$
$$x_2 = \frac{R_1R_5 + R_3R_5 + R_3R_4 + R_4R_5}{R_2R_4 - R_1R_5} $$
$$ x_1 = \frac{R_2R_4 + R_3R_5 + R_3R_4 + R_4R_5}{R_2R_4 - R_1R_5} $$
$$x_5 = \frac{R_1R_3 + R_1R_2 + R_2R_3 + R_2R_4}{R_2R_4 - R_1R_5} $$
$$W = \frac{R_3(R_1+R_2+R_4+R_5) + (R_2+R_5)(R_1+R_4)}{R_2R_4 - R_1R_5} $$
$$ L = \frac{R_3(R_1+R_2)(R_4+R_5) + R_1R_4(R_2+R_5) + R_2R_5(R_1+R_4)}{R_2R_4 - R_1R_5} $$
and finally
$$ R = L/W = \frac{R_1R_4(R_2+R_5)+R_2R_5(R_1+R_4)+R_3(R_4+R_5)(R_1+R_2)}{(R_2+R_5)(R_1+R_4)+R_3((R_1+R_2)+(R_4+R_5))}. $$
Interestingly, if the resistors $R_1, R_2, R_4, R_5$ all have the same value, say $\rho$, then it can be shown that the resistance of the entire circuit will not depend on $R_3$ at all and will instead just be equal to $\rho$.
I think this formula might help you:
$$R_3 \frac{R_1 + 3R_2}{R_4+3R_5}$$
