Equivalent Resistance

Question

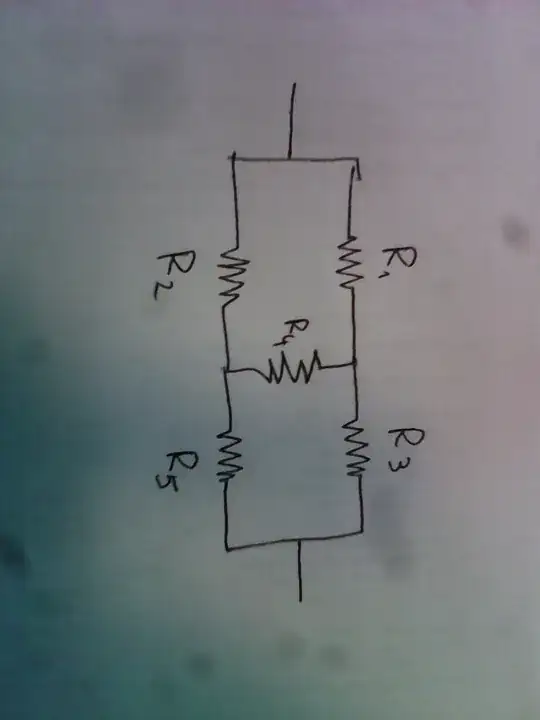
I've never had problems in finding the $R_{eq}$ of a circuit, but in this case I don't really know how to do it:

Answer 1

This is niether series nor parallel circuit, because of resistor 4. We have to use Kirchoff's laws. We will assume that both ends are connected to a battery to simplify our analysis.

First, reformulating the loop rule, we get that since the potential difference between the top and bottom end is the same, all paths from the top to bottom end must end up with the same potential difference, lets say $V$. There are four paths, (1,3), (1,4,5), (2,4,3) and (2,5). Hence, assuming the current through 4 to go to the left (if value is negative, then current goes to right) and that current goes from top to bottom,

$I_1R_1 + I_3R_3 = V$, $I_2R_2 + I_5R_5 = V$, $I_1R_1 + I_4R_4 + I_5R_5 = V$ and $I_2R_2 - I_4R_4 + I_3R_3 = V$

From Kirchoff's junction rule,

$I_1 + I_2 = I_3 + I_5$, $I_1 = I_4 + I_3$ and $I_2 + I_4 = I_5$

With these equations, we need to solve for $V/I_{net} = V/I_{before} = \frac{V}{I_1+I_2}$. From here it is just mathematics.