I am really confused please help me! I want to find the resistance between a and b! But i am not able to understand which resistances are in series or which are in parallel!
What i think- e and a are in series, then they are in parallel to c! Then c and d are in series and they are parallel to b! But the answer isn't correct!
Please tell me where i am wrong! Thank you ... and please tell like i told you my answer! 
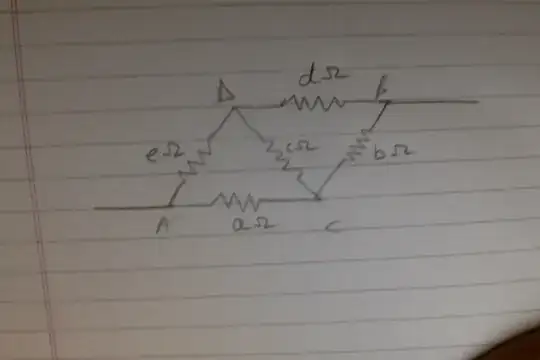
I can verify using Kirchoff's laws that this is solvable.
Ultimately, $$R_{equiv} = \frac{I_aa+I_bb}{I_a+I_e}$$ where the subscripts denote which resistor the current flows through.
Setting up $I_e = I_d+I_c$, $I_b = I_a+I_c$, $I_ee + I_cc - aI_a = 0$, $I_dd - bI_b = cI_c$, which is 5 unknowns, but only 4 equations. This isn't a problem, as you can soon see.
You can eliminate $I_c$ immediately, to get
$$ I_b = \frac{(a+c)I_a}{c} - \frac{e}{c}I_e$$
Now, using the other equations, $I_d$ can be eliminated as well:
$$ I_d = \frac{(c-e)I_e}{c}-\frac{a}{c}I_a $$
And, this leads to elimination of $I_e$
$$ I_e = \frac{ac+ad+ba+bc}{dc+be-ec-ed} I_a $$
Which I included in this problem just to explain that while I only have 4 equations, substituting into the resistance equation (first equation), you will see that everything is in terms of $I_a$, and $I_a$ can be factored out.
Since the resistance is a ratio of unknowns you can use Kirchoff's laws even if there isn't a voltage source, and even if it looks like you don't have enough equations. Ultimately, with n equations and n+1 unknowns, you can express all the unknowns in terms of one of the unknowns - and if you need to solve for a ratio of the unknowns, this can be solved for with the given equations.
