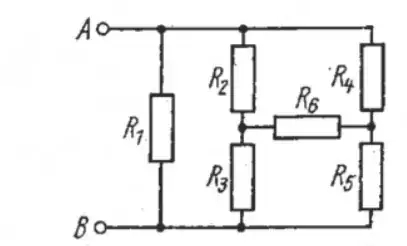
$R=R_1=R_2=R_3=R_4=R_5=R_6= 10 \Omega$ $R_2 \quad and \quad R_3 \quad with \quad R_4 \quad and \quad R_5 \quad are\quad in \quad series$
Therefore, $\frac{1}{R_{tot}} = \frac{1}{R_1}+ \frac{1}{R_2+R_3}+\frac{1}{R_4+R_5}= \frac{1}{R}+\frac{1}{2R}+\frac{1}{2R}= \frac{2}{R}$
$R_{tot} = \frac{R}{2}$
What I don't get is, why we can ignore $R_6$?
One approach to determining the effective resistance is to place a perfect source of emf, say E, across the terminals A and B. Then work out the current drawn by the battery, say I. If a battery of emf E draws a current I, then the effective resistance across the terminals is E/I. Because of the values of resistors you use, the potential difference across the resistor $R_6$ will be zero, so no current flows through this resistor and you can effectively remove this resistor from the circuit.
