0

To calculate the resultant resistance of a circuit can you use all possible paths and assume they're parallel?

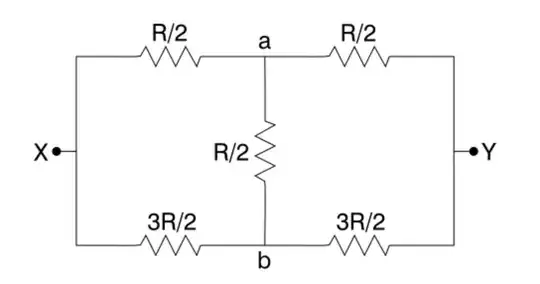
Say I have a circuit like this: enter image description here

And I want to determine the resistance between x and y. Is it valid to write down every possible path electricity could take (obviously without going back to the same node twice), and assume they're parallel?

Example of SOME possible paths here would be:

  1. R/2 + R/2
  2. R/2 + R/2 + 3R/2
  3. 3R/2 + R/2 + R/2

But this is NOT a possible path:

  1. R/2 + R/2 + 3R/2 + R/2 + R/2 corresponds to X -> a -> b -> X -> a -> Y

Is this a valid way of solving problems like this?

Also yeah I know how to solve this by saying a&b are at the same potential and going from there, I'm just curious if this more general way of solving is valid?

Qmechanic
  • 220,844
WilliamHarvey
  • 165

2 Answers2

0

No, that isn't a valid method of solution. It will not give the correct result.

There are four typical methods for solving this problem:

  1. Use the delta-wye transform on part of the circuit, to obtain an equivalent circuit that can be analyzed in terms of series and parallel combinations.

  2. Notice that the ratios $\frac{R/2}{R/2}$ and $\frac{3R/2}{3R/2}$ are equal, and therefore when a test voltage is applied between 'X' and 'Y', points 'a' and 'b' are always at the same potential. Therefore there will never be any current through the resistor connecting 'a' and 'b'. This means that resistor can be removed from the circuit without changing its behavior, leaving a circuit that can be analyzed in terms of parallel and series combinations.

  3. Use nodal analysis to analyze the circuit.

  4. Use mesh analysis to analyze the circuit.

Any of methods 1, 3, and 4 will also work even when the symmetry required for method 2 is not present.

The Photon
  • 29,651
0

yeah I know how to solve this by saying a&b are at the same potential and going from there

In that case you should be able to see immediately that your proposed method will give a different result, meaning it is incorrect.

If you remove the center resistor, you have only two parallel paths through the circuit: through two R/2 resistors and through two 3R/2 resistors.

Your proposal would be to also consider two additional paths through the circuit and consider them as in parallel with the previously mentioned paths. Adding any additional parallel paths can only reduce the equivalent resistance, giving a lower numerical result than the method you said you know is correct.

Therefore the proposed method must not be correct.

The Photon
  • 29,651