Why does holding something up cost energy while no work is being done?

Question

I read the definition of work as $$W ~=~ \vec{F} \cdot \vec{d}$$ $$\text{ Work = (Force) $\cdot$ (Distance)}.$$
If a book is there on the table, no work is done as no distance is covered. If I hold up a book in my hand and my arm is stretched, if no work is being done, where is my energy going?

Answer 1

While you do spend some body energy to keep the book lifted, it's important to differentiate it from physical effort. They are connected but are not the same. Physical effort depends not only on how much energy is spent, but also on how energy is spent.

Holding a book in a stretched arm requires a lot of physical effort, but it doesn't take that much energy.

• In the ideal case, if you manage to hold your arm perfectly steady, and your muscle cells managed to stay contracted without requiring energy input, there wouldn't be any energy spent at all because there wouldn't be any distance moved.

• On real scenarios, however, you do spend (chemical) energy stored within your body, but where is it spent? It is spent on a cellular level. Muscles are made with filaments which can slide relative to one another, these filaments are connected by molecules called myosin, which use up energy to move along the filaments but detach at time intervals to let them slide. When you keep your arm in position, myosins hold the filaments in position, but when one of them detaches other myosins have to make up for the slight relaxation locally. Chemical energy stored within your body is released by the cell as both work and heat.*

Both on the ideal and the real scenarios we are talking about the physical definition of energy. On your consideration, you ignore the movement of muscle cells, so you're considering the ideal case. A careful analysis of the real case leads to the conclusion that work is done and heat is released, even though the arm itself isn't moving.

* Ultimately, the work done by the cells is actually done on other cells, which eventually dissipates into heat due to friction and non-elasticity. So all the energy you spend is invested in keeping the muscle tension and eventually dissipated as heat.

Answer 2

This is about how your muscles work -- the're an ensemble of small elements that, triggered by a signal from nerves, use chemical energy to go from less energetical long state to more energetical short one. Yet, this obviously is not permanent and there is spontaneous come back, that must be compensated by another trigger. This way there are numerous streches and releases that in sum gives small oscillations that create macroscopic work on the weight.

Answer 3

Perhaps an analogy is in order. Lets hold up the book by using an electromagnet (say we put a piece if steel under it ). If the coils were made of superconducting material it would take no energy input to maintain the position/field strength. But if we use ordinary wire, ohmic loses within the coil must be made up for by externally supplied electrical energy.

Answer 4

The reason is that you need to spend energy to keep muscle stretched.

The first thing you need know is that the work $W=F \Delta x$ is the energy transfer between objects. Hence, there are no work done on the book when it is put on the table because there are no movement.

When your arm muscle is stretched, however, it consumes energy continuously to keep this state so you feel tire very fast. This energy comes from the chemical energy in your body and most of them are converted into heat and lost to the surrounding. In this situation, no energy is transferred to the book, so no work is done.

You can feel the different energy consumption when your arm is stretched in different angle. A particular case is that you put the book on your leg when you sit on a chair so your muscle is relaxed and the energy spent is less.

There are also a special type of muscle, smooth muscle, requires very little energy to keep its state so that it can always keep it stretched and you won't get tire:

Tonic smooth muscle contracts and relaxes slowly and exhibits force maintenance such as vascular smooth muscle. Force maintenance is the maintaining of a contraction for a prolonged time with little energy utilization.

Answer 5

When contracted, the sarcomeres, the structure that actually do the work in a muscle, take turns doing the work. Only a third of them are engaged at any given moment.

This is because the sarcomere pumps blood as it contracts and relaxes, enabling it to get the energy it needs to do its work for longer periods. The temporary, superhuman strength some people experience may be some sort of override of this normal level of engagement.

This system doesn't have a different mechanism for holding a position, so the same thing goes on when trying to hold an object steady.

But if the muscle is contracted for a very long time and the energy in the blood being pumped becomes insufficient, sarcomeres will actually get stuck in their contracted position. This state doesn't require energy and the sarcomere will remain contracted until the load stops and normal circulation is restored.

I believe this is a survival mechanism that enables an animal to hang on, even when the load would otherwise be overwhelming.

It also can cause muscle stiffness when circulation through a muscle is impaired, a very common condition as people age.

Answer 6

The big difference between holding up a book in your hand (by holding it in the palm) and holding up a book by laying it on a table is that the first equilibrium position is a dynamic one, while the book on the table is in a static equilibrium.

You can compare the situation in which you hold up a book with the situation in which a book is held up by constantly bombarding it from below with a huge number of small clay marbles. All marbles stick to the bottom of the book and give off all their kinetic energy to the book (which corresponds to the energy one uses to keep up the book in a steady-state in the palm of one's hand). The upward force is provided by the changes in momenta of the clay lumps.

So each time a marble hits the book it loses some of its kinetic energy (friction) and its momentum changes (providing the upward force). The friction energy is partly given to the book, which is slightly heated, just like a muscle is when contracted.

Now, where is the connection with the muscles keeping up the book? I think it's easy to see, though I don't have too much understanding of the muscles' workings. All muscle cells can be compared with the marbles (though, of course, the correspondence is far from exact). This correspondence can be made because the muscles (this I do know) relax, go tense, relax, go tense, etc. like the clay marbles provide small temporary forces. I think if a muscle cell wouldn't show this behavior (tense, relax, tense, relax...) the muscle cell would be static (which is different from a steady-state) and consume no energy (unless it is upheld by muscle cells that do show this behavior).

So a marble represents a muscle. The mass of these marbles depends, of course, on the velocity one gives to them and on the energy used in the cycle of muscle contraction and relaxation. The energy released when the marbles get deformed while attaching themselves to the book represents the energy released in the muscle cycles of contraction and relaxation. The upward force provided by the lumps of clay (the net change in momentum of the marbles per unit time) represents the force that the muscle cycles provide.

The book in your hands appears to be static but in reality, it finds itself in a steady-state, which, I think, is highlighted by the correspondence with clay marbles.

Answer 7

An analogy is the floating helicopter.

When it is static, no work is done to the helicopter.

But it is consuming the gas.

Answer 8

RL; DR: There is actual mechanical work done when holding a book.

Work depends on the reference frame
Let as consider an example of a motorboat going against the current in a river (this is somewhat similar to the helicopter example given by @Jian in another answer). If the speed of the boat is the same as the speed of the current, the boat will appear as static to the observer on the river bank, the force of its motor (and the friction force of water) does zero work. On the other hand, in respect to an observer on a raft, moving along with a current, the boat moves with the speed of the current, the force of its motor doing finite work. Btw, it is more practical in this context to speak of power, i.e., the work per unit time: $$P=\mathbf{F}\cdot\mathbf{v}.$$

Work can be done an a microscopic level
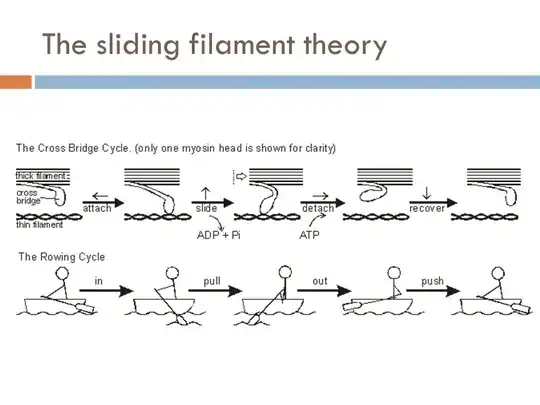
A muscle consists of fibrilles, containing structures called sarcomeres (see here for the figure explaining which is which, as well as the figure below). Within each sarcomere, in a process known as cross-bridge cycle, myosin (thick filament) pushes itself against actin (thin filament). This is a cyclic process which can be though of as myosin walking along actin, like a person walking up a descending escalator (here is a nice animation of this process). The process continues till the exhaustion of the chemicals, at which pont the filaments snap back to their initial positions.

The distance walked by myosin is hundreds of micrometers and the force of its pull is of the order of pico-newtons, however, as the muscle consists of many fibers, these forces add up to give the force necessary to hold a book. The large number of fibers is also the reason why, when in some of the fibers the filaments snap to their initial positions till the fibers recharge in chemicals, the muscle continues to exert force.

To put it on a more mathematical footing:
the work done by one myosin filament is $$ w=\mathbf{f}\cdot{d},$$ which gives us the total work, when it is multiplied by the number of simultaneously marching myosins: $$N\times w=N\times\mathbf{f}\cdot{d}.$$ Finally, if the filaments snap to their initial position after time $\tau$, the rate of energy dissipated by holding a muscle in a contracted position per unit time (i.e., the mechanical power), can be calculated as $$\frac{N\times\mathbf{f}\cdot{d}}{\tau}.$$

---

The image below (taken from this presentation) illustrates the analogy between the boat on a river and the cross-bridge cycle

Answer 9

Consider an analogy,

We get tired after STANDING for some time,without doing any work*. The reason behind this is same as the reason of why we dont do any work holding any object above our heads, but this case is easier to comprehend,

when we stand we r actually resisting the tendency of falling on the ground,muscles are holding on to the structure of our body so that we dont collapse on the ground like some non living thing,

these muscles have fibers which have have streached themselves ,which requires energy,

Similarly when we hold something above our head we r doing the same thing, resisting that collapsing tendency , which causes elongment in the muscles which requires energy.

Answer 10

Work is about energy transfer. The dot product in mathematical definition of mechanical work: $$W = \int \vec{F}\cdot d\vec{s}$$ makes sure that only the energy that is transferred from one thing to another is accounted for. If the force is constant, then the integral simplifies: $$W = \vec{F}\cdot\vec{s}.$$

an example

If we apply a force in the down direction (lets call it $-\hat{y})$ to a box that is moving horizontally (call it the $+\hat{x}$ direction), the force has no effect on the box. It still has exactly the same amount of kinetic energy before and after the force was applied.

Mathematically, $\vec{F}$ and $\vec{s}$ are perpendicular, so the their dot product is zero.

If we instead apply a force that is $45^\circ$ below the horizontal in the direction of motion, the force now has $\hat{x}$ and $\hat{y}$ components. But the displacement still only has an $\hat{x}$ component. $$\vec{F} = F_x \hat{x} - F_y \hat{y} \quad\quad\quad \vec{s} = s\,\hat{x}$$

When we do the dot product with $\vec{s}$, only the part of the force that adds energy to the box, $F_x$, will contribute to the work: $$W_\mathrm{on\,box} = \vec{F}\cdot\vec{s} = (F_x \hat{x} - F_y \hat{y})\cdot (s\, \hat{x}) = (F_x\,\hat{x})\cdot(s\,\hat{x}) - (F_y\,\hat{y})\cdot(s\,\hat{x}) $$ The second term vanishes, because $\hat{y}\cdot\hat{x} = 0$. Those unit vectors are perpendicular. Only the first term, where $\hat{x}\cdot\hat{x} = 1$, contributes to the work on the box.

So the work done on the box is $$W_\mathrm{on\,box} = F_x\, s.$$ The part of the force that we applied in the horizontal direction transferred energy from us to the box. We may have "used" some energy pushing in the $\hat{y}$ direction too, but that energy was wasted. It was not transferred to the box. We calculated the work done by us on the box, not the total energy expended by us.

holding a book

When you hold a book still, its energy is not changing. It has constant gravitational potential energy and no kinetic energy. If you drew a free body diagram for the book, there'd be two forces, gravity pulling down and you pushing up.

You could say that you are trying to give the book energy by pushing up, but gravity prevents you from succeeding. That's why you feel tired after holding a heavy book for a long time. The energy you spend doesn't go to the book, but it goes somewhere.

Work isn't the only way to transfer energy. When you physically exert yourself, chemical energy in your body is converted to mechanical energy and heat. When you hold a heavy thing for a while your body heats up and you might start sweating. The wasted energy becomes heat energy.

The energy your body spends to exert the upwards force is transferred to the environment as heat.

Answer 11

Actually, the work is being done, but only at the microscopic level. Imagine this if your hand didn't provide any support then the object would fall. So we do provide acceleration to the object (a=-g) towards the negative direction to overcome the normal force exerted by the book/object and the displacement is almost negligible that it is invisible. Remember if there is a change in Mechanical energy, there is always some work done in some form or the other. The normal force that your hand provides to the object microscopically repels the atoms of the box pushing them upward such that they appear at rest. And this is not just for a few seconds, this task has to be done in every instant of time otherwise the object would fall. So, the moment you lose your hand, the box would gain acceleration downward and again your body pushes it up, obviously assuming that still, you want to hold the object.

It is not necessary that work is done always if there is a visible motion or a visible consequence. Nor is this necessary that every motion requires work to be done.

Answer 12

$F=ma$ means that every force is applied to a mass and produces an acceleration. Okay. Acceleration is $a=\frac{\Delta v}{\Delta t}$. If you put this $\Delta v$ into ${\frac{1}{2}m(\Delta v)^2}$ you discover the energy which have been necessary to let that mass accelerate. Since energy is neither created nor destroyed, it is the energy burnt by the one who applied the force! His/her/its potential energy (e.g. from food) has become kinetic energy of the accelerated body. Now, what about holding up 5 kg with your arm? No energy? Of course you spend energy. It is the same as above: you apply a force, equal and opposite to the gravitational force, so the object doesn't fall and doesn't rise and if you apply a force, for the reason above, you spend energy. Now one could object that there is no acceleration in this case. If no acceleration (opposite to the gravitational acceleration $g$) existed, the object would fall! We have two opposite accelerations (since two opposite forces) at stake ($\mathbf{F}=-\mathbf{F_g} \Rightarrow \mathbf{a}=\mathbf{-g}$). Which cancel. But if they cancel they both exist. So yes, you spend energy for holding the object up: to let this counter-acceleration exist. So you need energy to hold up a mass but no work is done if the object is at rest on your hand, since its kinetic energy is NOT varying. If you stop with your hand a falling body you cause a negative $\Delta E_k$ (you do negative work on it) but once it is stopped no more work, your energy is simply to cancel $F_g$ and keeping the body at rest.

Answer 13

In my humble opinion, I don't really think this is much of a problem that needs so much clarification. You must understand that the "energy" you know in Physics has absolutely, I mean absolutely nothing to do with the energy that your body cells expend. You can actually expend energy while doing physical (of Physics) work but who cares! Physics only works with what it has defined to be "work" and if you don't do this kind of work believe me you haven't done any work as far as Physics is concerned. The definition of work in Physics would have told you already it doesn't depend on what you feel or what your cells do. It is just force and distance. You are exhausted because you climbed some stairs even though Physics would say you have increased your potential energy. So isn't that a contradiction! Why are you feeling weak when you have increased your potential energy? The bottom line is: physical work and the one you think is actually real work are just totally different. While the former was invented by physicists, the latter is what happens in your cells of which we don't care about as long as Physics is concerned.

Answer 14

Energy is being expended maintaining it in position. Earth's gravity is applying a force downwards, the book is being accelerated down gravitation force.

A force is being applied to the hand and arm which must be resisted and thus energy expended.

The arm and book are not a closed system.