In the limit, does walking slowly downstairs cost me as much energy as walking upstairs?

Question

I am not a physicist.

If I allow myself to roll down a hill, then apart from receiving bruises, I will expend no energy.

Having suffered ill-health recently, it seemed reasonable for me to restart my exercise routine by walking down the stairs from my 8th floor flat, but taking the lift (elevator) when going back up again. Surely walking down the stairs would be easier. However, because I was moving very slowly to begin with, it occurred to me that, by using my muscles to brake my descent, I was expending a considerable amount of energy.

Suppose I walk downhill hill very, very slowly and compare this with walking uphill at a similar speed. It seems to me that at any instant I am supporting my body weight on one foot and if I pause, this will be no different regardless of whether I am moving up or down.

Clearly if the speed of travel is zero then simply using my muscles to maintain my position is equal whether going up or down. At the other extreme, rolling/falling uses less energy than climbing.

Question

How does the speed of my descent affect the energy I expend by braking with my muscles? Is the relationship linear?

Is it even different from that of ascending?

---

Assumptions

I am not storing energy in my muscles when descending.

Braking is entirely dependent on muscle power and there is no slipping or sliding on the staircase.

I advance at a constant speed so there is no 'falling' from one step to another.

Answer 1

It's a tricky one! I will try to answer keeping math to a minumum and only introduce the concepts we need. This all can be modelled to be quantitative, let me know if you want me to. Also, let me point that the following is an explanation of why you also need to spend energy when descending in mechanical terms so its only a schematic view of how the human body works!

So, what is the point here?

Of course, one thinks going down is "free" and going up costs energy. And this is true: a free falling body accelerates because there is a force (gravity) acting on it and we know from Newton's second law that $$F=ma$$ where ofc $F$ is the force, $m$ the mass and $a$ the acceleration. There is no doubt that if your aim is simply to "go down", this helps you a lot as the external force (gravity) will "push" you!

However, you don't want to simply fall down: you want to walk down at constant speed!

Free-falling 8 floors (assuming 3 meters per floor, that's an height $h=24$ m) without somehow braking would mean reaching a final velocity $v_f$ of

$$v_f=\sqrt{2 g h} \approx 21 m/s = 70 km/h$$ that's the speed of a car (43mph) [I used $g=9.8m/s2$ for gravity].

So, you need to brake. How? Using your muscles.

Conversely, to climb the stairs, you need to work against gravity to go up.

Braking vs climbing

So, what's better, in terms of how much energy you require: climbing or braking?

If your aim is to go up or down at constant speed, which means zero acceleation ($a=0$) from Newton's law we get:

$$F=ma=0$$ implies that you have to have, in total, no force acting on your body. You already have a force which is due to gravity which is $mg cos(\theta)$, $\theta$ being the angle your stairs have wrt the horizontal plane, then your muscles have to exert the same amount of force! And that force is the same whether you are going up or down: in one case you exert it to move, in the other one to brake.

Funnily, your request of constant speed leads to the result that the force you need (that is proportional to the energy you spend, if the distance you travel is the same) is the same both ways.

Going through the assumptions

However, you deliberately asked us to neglect some facts (friction, etc). That's where the very interesting (and more realistic) bits are, so let's take them briefly into account:

• friction plays a role. Without friction you could not walk up- nor downwards. However, when going down, you might have friction doing a bit of the braking for you, decreasing the force you need. As an example, out of context, think of going down the stairs with a bike: you need to pedal a lot on the way up, but you can just hit the brakes on the way down! Despite the total energy expenditure being the same in both cases, on the way down friction (between the wheels and the brakes) are doing all the work and you simply need to operate the brakes. That also solves the "rolling down the hill" problem you posed: the friction between you and the hill is decreasing your speed allowing you to roll at a safe enough speed without having to spend energy to brake. However, the cost you have to pay is bruises/production of heat.

• you never really go at constant speed. The stopping and resuming motion one does when walking affect fatigue in different ways when going up or down. For example, when going down, one might 'run down' fast, having gravity lend you a lot of the energy and not braking much and then brake all of a sudden completely or partially. Depending on the specifics of how you do this kind of thing, the energy consumption may vary.

• another non-constant speed strategy might be using the "normal reaction" of the stair to brake you. Imagine you go down $N$ steps of height $h_0$: each of them will require you an energy $E\approx mgh_0$. Now, on the way back, you might just spend a tiny bit of energy $\varepsilon$ for walking, on a plane!, along the step, then "fall down" an height $h_0$, "hit" the next step and stop there, taking advantage of gravity to go down (i.e. you avoid spending the energy $E$ that you had to spend on the way up) and also ofthe fact that a small fall won't hurt you but it will brake you.

• the geometry of your stairs might play a big role in how big a step you need to do. In the previous model where one instead of going at constant speed just goes one step at a time, things might change a lot depending on how "high" each step is. That strategy for example is convenient if $\varepsilon <E=mgh_0$ i.e. if taking a horizontal step is for your muscles easier then taking a "upward" steps. For a very long and not very steep step (i.e. a step with small $h_0$ but in which you have to walk a lot to get to the next step) this might not be very convenient. Also, if $h_0$ is very high that might hurt you!

• sometimes what you care about is not the total energy and not the total force you need, but rather the power you are willing to give, i.e. how much energy per unit time. The slower you walk, the more your body has time to cope with fatigue. However, it will take you a longer time..

So, summing up, while there is no way you are going to spend less than an amount $mgh$ of energy to climb stairs up to a height $h$ and while it is true that the same amount will have to be "given back" to you by gravity on the way back, how much of that energy (and of the additional one due to friction) has to be provided by your muscles varies depending on several factors. In the assumption of constant speed, without taing steps etc., going up or down requires the same total amount of energy.

Also note that this answer we are neglecting how muscles work (e.g. they don't supply a continuous force but a "power stroke") and we are only focusing on you energy output. Because your body converts food water and air into energy with a given efficiency less than 100%, that means that you actually need even more energy/nutrients as an input. But that is regardless of going up and down.

Answer 2

Theoretically, if we keep the same slow constant velocity, the expended energy is the same for going upstairs or downstairs.

Walking down or up requires changing the angle between legs and thighs, under a force that is the weight of the body above the knees.

One way to measure the work is $\tau \times \theta$, the torque generated by that force times the change of the angle between leg and thigh. As the situation is symmetric going up or down, the energy should be the same.

But in reality, our body knows that gravity can help to go down, and let us make small "free falls" between steps, knowing that the friction between the bones at the knee and feet will hold each step impact.

That is why, I think, going downstairs may be harmful to knees than going upstairs.

Answer 3

I can give you an answer from experience as I have nerve damage to the point where walking is very difficult. Going down the five steps at my front door is much easier than going up them. Going down and collapsing my leg muscles slowly requires less effort, for me, than going up and having the leg muscles work to lift my weight. However as different muscles may be used in climbing and descending you should see which is harder for you, as individuals may have different strengths in different muscles. From a physics standpoint it requires work to increase gravitational potential.

Answer 4

When you are going down the stairs, the only reason your feet would have to expend any force would be to balance mg and normal force.

When you are moving up, your feet push you up, working against both mg and normal reaction exerted by the stair.

Answer 5

You've received a lot of incorrect answers so far. Let's start with some definitions. As you walk up or down stairs, let the change in your gravitational potential energy be $U$, and let the amount of food energy you burn be $E$. Define $C_\text{vert}=E/U$, the vertical cost of walking. Conservation of energy requires only that $E\ge U$. So when you go up stairs, with $U>0$, we must have $C_\text{vert}\ge 1$, and when you go down, $C_\text{vert}\le 1$.

Pretty much everything I've said so far is very generic, so it would apply equally well to any machine. This is the problem with the answers by JalfredP, Math_Whiz, and Claudio Saspinski, which attempt to explain what's going on in the human body without using any facts about how the human body differs from other machines. This is doomed to failure. An electric car going downhill has $C_\text{vert}>0$, because it recharges the battery with regenerative braking. A human body going downhill has $C_\text{vert}<0$, because you still burn calories even when walking downhill. There is no generic explanation of these facts that can be based simply on the principles of mechanics, without saying something about the nature of the machine involved. There is nothing in the principles of newtonian mechanics or conservation of energy that prevents me from building a battery-powered anthropomorphic robot that uses regenerative braking when it walks down stairs.

Let's look at some real data on the human body. Minetti (2002) measured this sort of thing for elite mountain runners running on a treadmill inclined at a gradient $i$ ($i$ is the tangent of the angle). Their energy consumption $E$ was determined by measuring the amount of oxygen they consumed. The quantity $C_\text{vert}$, considered as a function of $i$, blows up at $i=0$, where $U=0$. Therefore it's nicer to look at the quantity $C=E/m\ell$, where $m$ is the person's body mass and $\ell$ is the distance traveled. If you're climbing straight up or down a ladder, then $C=gC_\text{vert}$. $C$ is always positive because $\ell$ is positive by definition, and the human body can't have $E<0$ like a Prius.

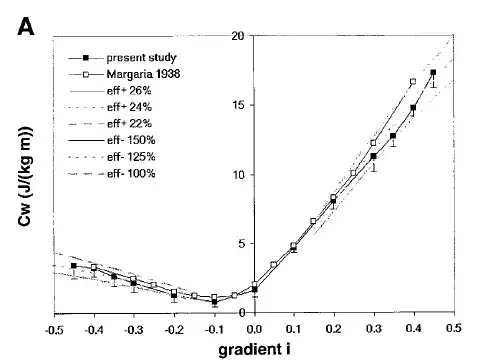
On steep uphill slopes, the observed value of $C_\text{vert}$, in these elite runners, is very close to what you would get just from the efficiency of muscle fibers. For sedentary people, it's worse by almost a factor of two.

In the limit, does walking slowly downstairs cost me as much energy as walking upstairs?

No, as you can see, the cost is far less.

How does the speed of my descent affect the energy I expend by braking with my muscles? Is the relationship linear?

Approximately, but not exactly. For running, Minetti found that this was true to a good approximation. This is what we would expect if the efficiency was independent of speed. However, there is no fundamental physics principle that dictates that this should be so. It's just an approximate observation about the human body. In general, if you take a frog's leg muscle and stimulate it, both the force it can generate and its efficiency do depend on the speed.

If you want a physics explanation of why the human body has the behavior described above, then this seems to have been partly figured out in recent years, but it's pretty complicated and there are a lot of unknowns. In general, during exercise, a lot of the food energy is being transformed into heat, and some of it is also going into endothermic chemical reactions. Only what's left over is available to do mechanical work. At the microscopic level, the smallest structural units of a muscle are proteins called sarcomeres. These include myosin, actin, and titin. There is something called the sliding filament theory, which was advanced in 1954. When you go downstairs, your muscles are doing negative work, which physiologists refer to as an eccentric contraction. In recent years, people have been working on explaining why the sarcomeres have the energy efficiency they do in eccentric contractions, and there are a couple of hypotheses available, both of which may be true. There is something called the winding filament hypothesis, illustrated below with a figure from Hessel.

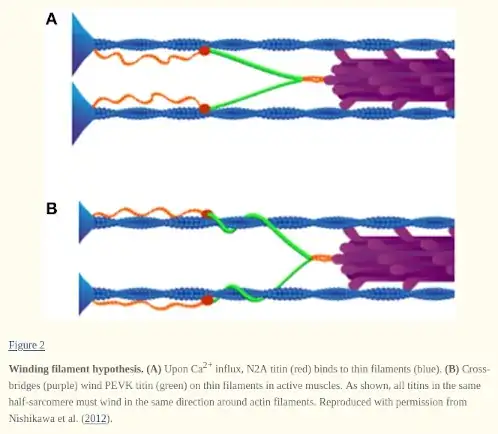
I don't know enough about the biophysics to be able to understand all the details. This is just meant to point you in the direction of the general type of explanation that is required here, which is an explanation involving the details of the machine, not general principles about newtonian mechanics. The classical observations, going back about a century, are that muscles in eccentric contractions are capable of generating large forces at low energy cost, where low energy cost means that $|C_\text{vert}|$ is small. If I'm understanding Hessel in a vaguely correct way, then I think the idea is that titin gives the muscle some mechanism that during a concentric (shortening) phase allows the fiber to stiffen, and then during the eccentric phase this stiffness lets the muscle supply a force at a low energy cost.

References

Minetti et al., http://jap.physiology.org/content/93/3/1039.full

Hessel et al., Front Physiol. 2017; 8: 70, https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5299520/ , doi: 10.3389/fphys.2017.00070

Related

Why does holding something up cost energy while no work is being done?

Answer 6

Every motor (I mean a generic machine which is able to convert energy from one form to another, so also a human can be considered a motor which turns chemical energy into kinetic energy) has a rate of return. The rate of return tells how much of the ingoing power is effectively turned into the new form of power and how much is dissipated (lost) during the process of transformation. The rate of return of a motor depends on a lot of parameters (for example think about the decrease of efficiency of an electric motor with the growth of temperature); however if you want to make estimates it is useful to consider a constant value for the rate of return. That said, you can call $\eta_{up}$ the rate of return of a human which is walking up the stairs or whatever you want (a hill...), and $\eta_{down}$ the rate of return of a human which is walking down. Note that I consider the two rates different because the kinematic and the muscles involved in the two scenarios are different. Moreover they will depend on a lot things like the shoes and the clothes you wear, the way you move your feet...
In order for a man to walk uphill it is necessary a certain minimum power, let's call it $P_{up}$ which refers to lowest speed one can move with continuity. $P_{up}$ will depend on the weight of the person, on his level of training and on the slope of the hill. Similarly $P_{down}$ is the minimum power necessary for a man to walk downhill and will have similar dependencies.
So, if you walk uphill very slowly your body will have to provide $P_{burnt/up}$: $$P_{up}=P_{burnt/up}*\eta_{up} \rightarrow P_{burnt/up}=\frac{P_{up}}{\eta_{up}}$$ If you walk downhill very slowly your body will have to provide $P_{burnt/down}$: $$P_{down}=P_{burnt/down}*\eta_{down} \rightarrow P_{burnt/down}=\frac{P_{down}}{\eta_{down}}$$ It is however not possible to provide real numbers for these quantities, and you also noted how many dependencies you should consider if you would like to have some real estimates. In this case the experimental way is the only possibility to achieve some good results; I did that theoretical excursus just to show you how to handle the problem and to show that your question can't be answered without some experimental measurements.