Questions tagged [feynman-diagrams]

Feynman diagrams were introduced by physicist Richard Feynman in 1948 to represent pictorially the mathematical expressions describing the quantum behaviour of subatomic particles. For example, the following graph represents a Feynman diagram:

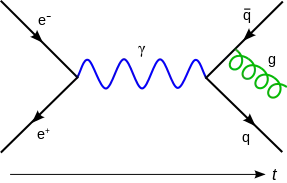
^{https://en.wikipedia.org/wiki/File:Feynmann_Diagram_Gluon_Radiation.svg}

Here, an electron and a positron annihilate, producing a photon (represented by the blue sine wave) that becomes a quark-antiquark pair, after which the antiquark radiates a gluon (represented by the green helix).

Introduction.

Feynman diagrams were introduced as a diagrammatic technique to keep track of the different terms that appear in the perturbative expansion of certain transition amplitudes in quantum mechanics. A primitive version of the technique was already being used by Stückelberg in his analysis of covariant perturbation theory, but the systematisation and popularisation of the method was a task undertaken by Feynman.

The problem was the following: given a Hamiltonian $H$ that describes a certain system, one wishes to compute its spectrum. To this end, it can be proven that it suffices to calculate the so-called propagation amplitude: $$ \langle q;t|q';t'\rangle=\langle q|\mathrm e^{iH(t-t')}|q'\rangle $$ where $q,q'$ are position eigenstates. In general, the Hamiltonian $H$ cannot be explicitly diagonalised (being a very complicated problem), so one contents oneself with approximating its spectrum in perturbation-theory. The procedure is typically the following: we assume that we can write $H=H_0+V$, where $H_0$ is a Hamiltonian whose spectrum is known, and where $V$ is small (say, in the sense that it is multiplied by a small coupling constant). In this situation, the perturbative expansion of $\langle q;t|q';t'\rangle$ can be written schematically as $$ \langle q;t|q';t'\rangle\sim K_0+K_0VK_0+K_0VK_0VK_0+\cdots $$ where $K_0(q,t;q',t')\equiv \langle q|\mathrm e^{iH_0(t-t')}|q'\rangle$ is the propagator of $H_0$, and each term represents a symbolic expression that contains iterated integrals of $K_0$ and $\langle q|V|q'\rangle$. In practice, the computation of the different terms in this series expansion can become very cumbersome very fast.

In his work, and inspired by some remarks made by Dirac, Feynman introduced a new formalism that we now call the path-integral formalism (or functional-integral for more generality). Using this new tool, Feynman was able to write down an algorithm to compute the transition amplitude $\langle q;t|q';t'\rangle$ as a power series expansion in the coupling constant. The algorithm had the advantage over old-school methods in that it was explicitly covariant and much more efficient (in that it avoided redundant terms that only differ in the name of the dummy variables). The path-integral offered an alternative expression for the transition amplitude: $$ \langle q,t|q',t'\rangle\equiv\int \mathrm e^{-i\int (H(\tau)-p(\tau)\dot q(\tau))\mathrm d\tau}\ \mathrm dq\;\mathrm dp $$ which, when expanded in a power series in $V$, leads to the exact same terms as the old-school approach.

The path-integral was a completely new mathematical object, which was regarded with some skepticism and unfamiliarity by Feynman's peers. Dyson was able to prove that the technique was nevertheless completely equivalent to the old-school methods, which helped convince the community of the convenience of the new approach. For this reason, the diagrammatic technique is sometimes referred to as the Feynman-Dyson expansion.

In any case, either directly from the path-integral or following the old-school method, the perturbative expansion of the transition amplitude can be written as a power series in the coupling constants, where each term consists of a combination of propagators and powers of $V$. Feynman organised the expansion in graphical terms as follows: each propagator is associated with a line, and each factor of $V$ to a vertex. To compute the transition amplitude to a given order, one draws all graphs with that many vertices and connects them using lines. From the graph, one can read, by means of a certain set of rules, what is the value of the term in the perturbative expansion. A collection of different Feynman diagrams can be found on the Wikimedia page on Feynman diagrams.

Field theory.

An advantage of the path-integral approach is that its generalisation from standard quantum-mechanics to quantum-field-theory is rather straightforward. What's more, as the path-integral is naturally written in terms of the action of the system rather than its Hamiltonian, the framework deals easily with Lorentz invariance, making it the most convenient tool to study relativistic quantum mechanics and particle-physics. Nevertheless, the framework is also convenient in the study of non-relativistic field systems, as in condensed-matter.