Could somebody explain how one can derive the symmetry factor both by counting possible contractions and by looking at the symmetry of a diagram. Consider for example this diagram
in $\phi^4$-theory with $\mathcal{L}_\text{int} = -\frac{\lambda}{4!}\phi^4$.
EDIT: the correct answer is this one.
My examples appear correct just because in this simple case (and in a few others) the method I presented ends up calculating the $|G|$ factor that the other answer mentions; it does not work in general, with any number of vertices or external legs (and if a method only works "sometimes", we can safely say that it doesn't work).
I will just leave it here for completeness of discussion.
The procedure is quite simple: the symmetry factor counts how many of the same diagrams you would be counting if you didn't consider that the single particles in your diagrams are identical. To do this, ask yourself "how many of this same diagram can I make?" where "same diagram" means "same external particles, same connections, and same vertices". To do this you want to
To work with your example in $\lambda\phi^4$ theory: 
Or yet another example: 
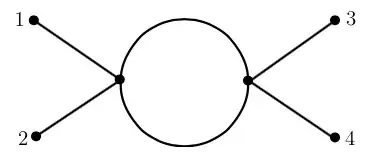
First a warning: Despite 19 upvotes and no correction for 3 years, Mauro's answer is wrong, which shows just how confusing symmetry factors are. I do thank Mauro for giving me the inspiration for the picture below. Mauro's method gives the correct answer for his two examples, but it looks like an accident, as the method is incorrect for the one-loop diagram with one vertex and two external edges, or for the figure 8 vacuum bubble, or for various other diagrams.
I will give a foolproof method to determine the symmetry factor. I will then give the see-it method and how the two methods relate (thus elaborating on this answer). I personally prefer the foolproof method, as it actually leads to understanding. I will present it for $\frac{\lambda}{4!}\phi^4$ theory, but the method easily generalizes.
Let's say you have a diagram with $V$ vertices and $n$ external edges.
When computing an $n$-points function, the factor to put in front of your diagram is $$\frac{C}{V!*(4!)^V},$$ a fraction of two large numbers which typically largely cancel out (see below), yielding 1/`the symmetry factor'.
Here, $C$ is the number of full contractions of $\phi(x_{\text{ext},1})\cdots\phi(x_{\text{ext},n})\int\phi(x_1)^4{\rm d}x_1\cdots\int\phi(x_V)^4{\rm d}x_V$ that yield the given diagram when attaching $x_{\text{ext},k}$ to the $k$th external edge (recall that in a Feynman diagram the vertices are indistinguishable, and for each vertex the outgoing half-edges are indistinguishable, but the external edges are actually distinguishable or `fixed', when you are interested in $n$-points functions $\langle\phi(x_{\text{ext},1})\cdots\phi(x_{\text{ext},n})\rangle$ as I'm assuming.)
In math terms: Every partition of $\{1,\ldots,n+4V\}$ into blocks of two can be mapped to a Feynman diagram by drawing an external half-edge for the elements $1,\ldots,n$, drawing a vertex with four half-edges for $n+1,\ldots,n+4$, another for $n+5,\ldots,n+8$, et cetera, until the last vertex with half-edges $n+4V-3,\ldots,n+4V$, and finally connecting all the half-lines that are in the same block of the partition. With regards to this map, $C$ is the number of partitions of $\{1,\ldots,n+4V\}$ into blocks of two, that are in the pre-image of your diagram.
Where does it come from? The numerator $C$ comes from Wick's theorem, or more precisely Isserlis' theorem. The denominator comes from expanding the exponential of $\frac{1}{4!}\int\phi^4$ in the usual way: you get terms $\frac{1}{V!}(\frac{1}{4!}\int\phi^4)^V$. The funny thing is, you could have chosen a different prefactor than $1/4!$ and ended up with different rules for symmetry factors.
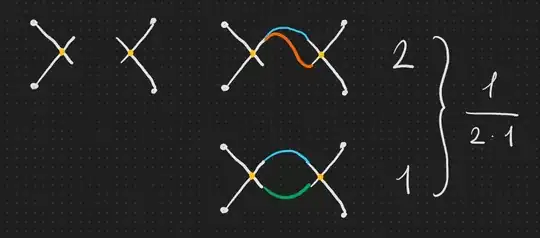
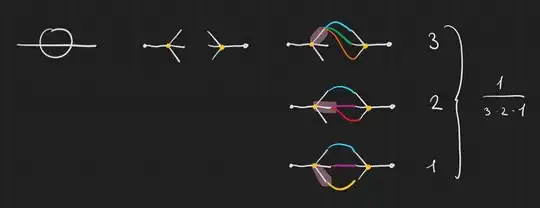
How to do it in practice? To calculate $C$, I start with drawing the external half-lines (I number them to make it clear that they are distinguishable), and I draw the vertices with their four half-lines. Then I connect the half-lines one by one, while multiplying the number of possibilities of connecting the half-lines for which you would be able to get the same graph: see the picture below. I start with connecting external line number 1. It always adds a factor of $V*4$. (Check if you see why!) Then I connect external line number 2, which always either adds a factor of $(V-1)*4$ or a factor of 3. (Check!) I keep going until all half-lines are connected. In the resulting fraction I keep as much small factors as possible (I write 3*4 and not 12) so that I can easily cross out factors between numerator and denominator. In the OPs example: $$\frac{2*4*3*4*3*2}{2!*(4!)^2}=\frac{1}{2}$$
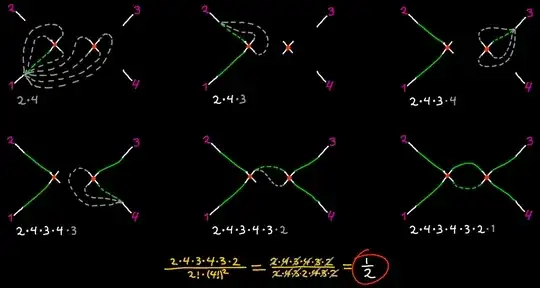
Tip: try all the diagrams in the image included in this question so that you can check your answer.
I kind of want you to stop reading here, and just go practice. But the OP asked for it, so here is the second method and its relation to the first.
By some math, you can show that $$\frac{C}{V!*(4!)^V}=\frac{1}{|G|},$$ where $G$ is a certain group of automorphisms, defined below. Computing $|G|$ can be faster once you understand it, but it causes much confusion because authors often don't mention that it secretly employs what I call `fully marked diagrams'.
Fully marked diagrams: In a Feynman diagram, the external edges are distinguishable - for clarity, let us mark them by the numbers $1,\ldots,n$ - but the half-edges on each vertex are indistinguishable, and also the vertices are indistinguishable from each other. In contrast, a fully marked diagram is a Feynman diagram in which we moreover mark the vertices $(1),\ldots,(V)$ and we mark their half-edges $(k,1),(k,2),(k,3),(k,4)$ for all $k=1,\ldots,V$, so that they become distinguishable.
Let $F$ be the map from fully marked diagrams to normal Feynman diagrams by forgetting the markings on the vertices and the internal half-lines.
Let $D$ be any fully marked diagram that is in the pre-image $F^{-1}(\Gamma)$ of your given diagram $\Gamma$. The lines of $D$ induce a partition $P$ (in blocks of size 2) on the half-lines of $D$. The vertices of $D$ induce a partition $\mathcal{V}$ (in blocks of size 4) on the internal half-lines of $D$. Now $G$ is the group of bijections of half-lines of $D$ that leave:
Now $|G|$ is your symmetry factor.
How to do it in practice? You look at your diagram, and you imagine that all half-lines are positioned at distinguishable places, let's say each 'place' has a distinct number, and the lines induce a partition on those place-numbers into blocks of two. Then you imagine rearranging the internal half-lines, to position them at potentially other places, but each half-line must stay with their original three neighbour-half-lines on the vertex (in principle, the half-lines may 'jump' to another vertex, but only if they do it with all four of them together, and this is rare). Moreover, you imagine the lines being dragged along with the half-lines. This induces a new partition on the place-numbers. If the new partition is the same as the old, then the rearrangement is valid. The symmetry factor is the number of valid rearrangements you can make. In the OPs example, the only valid rearrangements are the trivial rearrangement (when you do nothing) and the rearrangement that makes the top line and bottom line swap places. So we get $$\frac{1}{|G|}=\frac{1}{2}.$$
Why does this work? Note that $C$ is the number of contractions, i.e., the number of partitions $P$ that yield the given diagram. Each such partition $P$ corresponds in a 1-to-1 way to a fully marked diagram $D$ in $F^{-1}(\Gamma)$. Hence $C=|F^{-1}(\Gamma)|$, and we will now look at a different way to count the number of elements in $F^{-1}(\Gamma)$. For each two fully marked diagrams $D$ and $D'$ in $F^{-1}(\Gamma)$, one can obtain $D'$ from $D$ by rearrangement of half-lines, that is, a bijection of $X=\{1,\ldots,n+4V\}$ fixing $\{1,\ldots,n\}$ that preserves the vertex-partition $\mathcal{V}$. One checks that there are precisely $V!*(4!)^V$ such rearrangements. But some of these rearrangements send $D$ to $D$. By definition, those are the 'valid' rearrangements, and there are $|G|$ of those. Moreover, this number is irrespective of the chosen $D$ from $F^{-1}(\Gamma)$. Hence there are $\frac{V!*(4!)^V}{|G|}$ distinct elements of $F^{-1}(\Gamma)$, and therefore, $C=\frac{V!*(4!)^V}{|G|}$, equivalent to what was claimed.
My two cents: I prefer the first method because it has a direct link to where it comes from, helping fundamental understanding. I see the second method as a clever quick trick, intended to make life easier, but it is too often used without stressing that it uses a different and quite artificial type of isomorphism. Without proper explanation, each time a Feynman diagram passes on the blackboard, the student is left wondering whether its vertices are truly indistinguishable or not. The take-home message should be that Feynman diagrams are just Wick contractions.
Keep the external points $x_i$ fixed and look at the exchanging of propagators for the virtual particles. In this case there the factor is $2$ since you can only exchange them once and get the same diagram.
