Problem understanding the symmetry factor in a Feynman diagram

Question

I am trying to understand a $1/2$ in the symmetry factor of the "cactus" diagram that appears in the bottom of page 92 In Peskin's book. This is the diagram in question (notice that we are in $\phi^4$ theory)

In the book it is claimed that the symmetry factor of the diagram is

$$3!\times{}4\dot{}3\times{}4\dot{}3\dot{}2\times{}4\dot{}3\times{}1/2$$

where it says that the $3!$ comes from interchanging the vertices, the first $4\dot{}3$ from the placement of contractions in the $z$ vertex, the following $4\dot{}3\dot{}2$ from the placement of contractions in the $w$ vertex, the last $4\dot{}3$ from the placement of contractions in the $u$ vertex and the final $1/2$ from the interchange of $w-u$ contractions.

It is this last $1/2$ that I don't understand. Can you be more explicit on where this comes from?

Answer 1

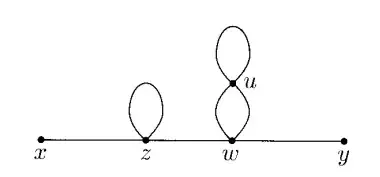
We choose one of the $4$ z-fields to contract with the single x-field. We then choose one of the remaining $3$ z-fields to contract with one of the $4$ w-fields. The remaining two z-fields just contract with themselves. Now choose one of the remaining $3$ w-fields to contract with the single y-field.

(Here is where we have to be careful). There are $2$ choices for the w-field contraction with one of the $4$ u-fields, and then $3$ choices for the other w-u contraction. In computing this last combination we have over counted by a factor of $2$.

To see this more clearly, consider one of the contractions,

$\phi_a(w)\phi_b(w) \quad\phi_a(u)\phi_b(u)\phi(u)\phi(u)$

The subscript denote which fields are contracted with which other fields (I'm not sure how to express contractions in Latex).

There are two ways to get this particular contraction: we could either choose the first w-field to be contracted with the first u-field, and THEN choose the second w-field to be contracted with the second u-field; OR we could choose the second w-field to be contracted with the second u-field, and THEN choose the first w-field to be contracted with the first u-field.

Clearly both of these are equivalent. However, in the combinatorics we have counted both of them, and so we must divide by a factor of $2$. So the total number of different contractions giving the same expression as $(4.45)$ is

$3! \, \times \, 4 \cdot 3 \, \times \, 4 \cdot 3 \cdot 2 \, \times \, 4 \cdot 3 \, \times \, 1/2$

Where the $3!$ comes from the interchange of vertices.

EDIT: If that isn't clear, think about the following scenario. There are two boxes, in the first there are two objects, $A$, and $B$, and in the second there are two more, $C$, and $D$. How many different ways are there to pair off the objects so that each object in the first box has a partner in the second box? Clearly the answer is two: $A,C$ and $B,D$; and $A,D$ and $B,C$.

One might think the answer is $2\cdot 2$, but we can see that this produces duplicates

\begin{array}{|r|r|} \hline First Pair & Remaining Pair \\ \hline A,C & B,D\\ \hline A,D & B,C\\ \hline B,C & A,D\\ \hline B,D & A,C\\ \hline \end{array}

So we must multiply by a factor of $1/2$ to fix the overcounting.

Hope that helps.

Answer 2

I don't think the explanation in the book is clear, but you can just ignore it and get the correct factor $S=\frac{1}{8}$ as follows.

1. Start by drawing 5 isolated vertices, two labelled ones with degree one and three unlabelled 4-valent vertices. Then $$ S=\frac{1}{3!}\left(\frac{1}{4!}\right)^3\times C $$ where $C$ is the number of contraction schemes that produce the given graph shape. The three vertices play different roles in the graph so one has $3!$ ways of choosing this role assignment (who is the nearest neighbor of $x$ etc.). Then a factor of $4$ for the $z$ leg that $x$ attaches to. Likewise, a factor of $3$ to choose which of the remaining $z$ legs moves on to $w$. Then at $w$ there is a factor of $4\times 3$ to choose the legs which receive the $z$ and $y$ edges. Then a factor of $6$ to pick which pair of legs at $u$ will form the tadpole. Finally there is a factor of $2$ to connect the remaining free legs at $u$ with the two remaining ones at $w$. Thus $C$ is number in your question.
2. Alternatively $S=\frac{1}{|G|}$ where $G$ is the automorphism group of the graph. More precisely, let $E$ be your favorite set with $14$ elements (the half-edges in the picture). Equip $E$ with two set partitions $\mathcal{V}$ and $\mathcal{E}$. The latter is made of $7$ disjoint pairs corresponding to the edges. Whereas $\mathcal{V}$ is made of two singletons and three blocks of four elements. Here $G$ is the group of permutations of $E$ which preserve the set partitions $\mathcal{E}$ and $\mathcal{V}$ and also fix the external legs (which here is automatic because the picture is asymmetric in $x$ and $y$). It is generated by three commuting order $2$ elements. For each tadpole you can permute the corresponding half-legs. Finally there is the exchange of the two edges between $w$ and $u$.

Answer 3

The 1/2 comes from the symmetry of the diagram. In the sense that if you look away and I switch the two propagators it is a "different" diagram, but you cannot tell. The numbers of ways to do this is 2.

If these were directed propagators it would not be the case.