17

If there is a system, described by an Lagrangian $\mathcal{L}$ of the form

$$\mathcal{L} = T-V = \frac{m}{2}\left(\dot{r}^2+r^2\dot{\phi}^2\right) + \frac{k}{r},\tag{1}$$

where $T$ is the kinetic energy and $V$ the potential energy, it is also possible to define the total energy $E$ of the system

$$ E = T + V =\frac{m}{2}\left(\dot{r}^2+r^2\dot{\phi}^2\right) - \frac{k}{r}.\tag{2}$$

If the angular momentum $M$ is defined by $$ M = m r^{2} \dot{\phi},\tag{3}$$ then $E$ can be written as

$$ E = \frac{m}{2}\dot{r}^2 + \underbrace{\frac{M^2}{2mr^2}-\frac{k}{r}}_{V_\textrm{eff}\left(r\right)},\tag{4}$$

where the last two terms are written as new, "effective" potential $V_\textrm{eff}\left(r\right)$.

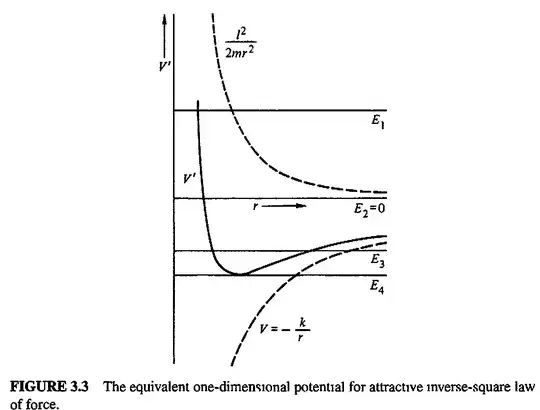
In addition, using the definition of $M$, the Lagrangian $\mathcal{L}$ can be written as

$$ \mathcal{L} = \frac{m}{2}\dot{r}^2 + \underbrace{\frac{M^2}{2mr^2}+\frac{k}{r}}_{-V_\textrm{eff}\left(r\right)},\tag{5}$$

where the sign of $V_\textrm{eff}\left(r\right)$ has been changed, since $\mathcal{L} = T-V$. But from this argument, it appears that there are two different possible ways to construct the same effective potential. This seems to me contradictory. Where is my mistake?

Qmechanic
  • 220,844
Aaron Wild
  • 377

2 Answers2

20

  1. The underlying reason for OP's flawed argument is that a premature use of EOMs in the stationary action principle $$\begin{align} S~=~&\int\!\mathrm{d}t ~L(r,\dot{r};\theta,\dot{\theta}), \cr L(r,\dot{r};\theta,\dot{\theta})~=~&\frac{1}{2}m(\dot{r}^2 +r^2\dot{\theta}^2) -V(r),\end{align}\tag{A}$$ invalidates the variational principle, cf. e.g. this Phys.SE post. Concretely, OP is achieving the incorrect Lagrangian $(5)$ by eliminating the angular coordinate from the original Lagrangian $(1)$ via the fact that the angular momentum $(3)$ is a constant of motion (which is the EOM for the angular coordinate).

  2. Now, for OP's example, it turns out that a correct reduction can be performed via the Hamiltonian formulation $$ H(r,p_r;\theta,p_{\theta}) ~=~\frac{p_{r}^2}{2m}+ \frac{p_{\theta}^2}{2mr^2} + V(r). \tag{B}$$ Note that the canonical momentum $p_{\theta}$ (which is the angular momentum) is a constant of motion because $\theta$ is a cyclic variable.

  3. We next re-interpret the system $(\text{B})$ in a rotating frame following the particle with fictitious forces and only 1D radial kinematics. The Hamiltonian $(\text{B})$ becomes $$ H(r,p_r)~=~\frac{p_r^2}{2m}+ V_{\rm cf}(r)+ V(r), \tag{C}$$ where $$ V_{\rm cf}(r)~:=~\frac{p_{\theta}^2}{2mr^2} \tag{D}$$ is a centrifugal potential in a 1D radial world, cf. my Phys.SE answer here. Hence, the Hamiltonian system $(\text{C})$ has effectively only one radial degree of freedom.

  4. Finally, perform a Legendre transformation on the Hamiltonian $(\text{C})$ to obtain the corresponding 1D Lagrangian system: $$ L(r,\dot{r})~=~\frac{m}{2 }\dot{r}^2\color{Red}{-}V_{\rm cf}(r)-V(r).\tag{E} $$ Note the crucial minus sign marked in red. One may check that the corresponding EL eq. for $(\text{E})$ is the correct EOM.

  5. The Lagrangian $(\text{E})$ is minus Routhian, cf. this Phys.SE post.

M. A.
  • 2,039
  • 5
  • 11
  • 28
Qmechanic
  • 220,844
3

Effective potential is defined by the formula $E=T_{radial}+V_{eff}(r)$. Your calculation shows that once you make this identification it is not true that $\mathcal L = T_{radial}-V_{eff}$, but that is fine. This happens because centrifugal term (i.e. the one with angular momentum) is really kinetic term and not a true potential. Hence it must enter the Lagrangian with plus sign, unlike the "real" potentials.

Blazej
  • 2,267