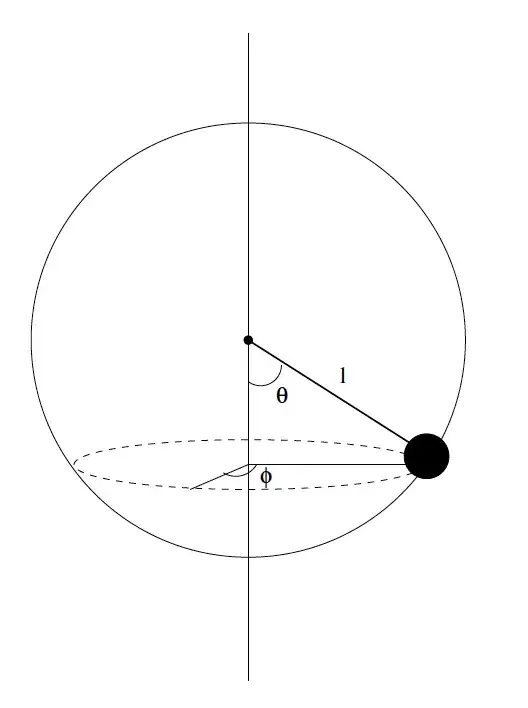
I am trying to solve for the equations of motion to simulate a spherical pendulum. I decided to use the spherical coordinates. The Lagrange equation is, $$ L=T-V=\frac{1}{2}m\left(l\dot\theta\right)^2+\frac{1}{2}m\left(l\sin\theta\dot\phi\right)^2-\left(-mgl\cos\theta\right), $$
where $l$ is the length of the rope, $ϕ$ is the angle of the projection of the rope on $x$-$y$ plane with $x$-axis and $θ$ is the angle with the $-z$-axis.
Now, From Noether's theorem, we know that the quantity
$$ J=\dfrac{\partial L}{\partial \dot{\phi}}=ml^2\dot{\phi}sin^2\theta $$ is constant. The equation of motion for $\theta$ follows from the Lagrange's equations and is
$$ ml^2\ddot{\theta}=ml^2\dot{\phi}sin\theta cos\theta-mglsin\theta $$ We can substitute $\dot{\phi}$ for the constant J in the expression to get an equation entirely in terms of $\theta$ which we choose to write as
$$ \ddot{\theta} = -\frac{\partial V_{eff}}{\partial \theta} $$
where the effective potential is defined to be
$$ V_{eff}(\theta) = -\frac{g}{l}cos\theta + \frac{J^2}{2m^2l^4}\frac{1}{sin^2\theta} $$
Now, if I had substituted J for $\dot{\phi}$ directly into the Lagrangian and solved, I would've derived a similar equation as above, but I would've got a minus sign wrong. And apparently the reason is that Lagrange's equations are derived under an assumption that $\theta$ and $\phi$ are independent. I do get that. But since we get $J$ from the Lagrangian, shouldn't substituting $J$ back and solving still work?
I am looking at this as just a mathematical operation and cannot seem to wrap my head around it. Could somebody give me a stronger reason as to why this doesn't work or maybe explain the above reason more explicitly?