I am trying to create a graph of effective potential for the Earth-Moon system in Excel. It should result in a graph that looks like this:
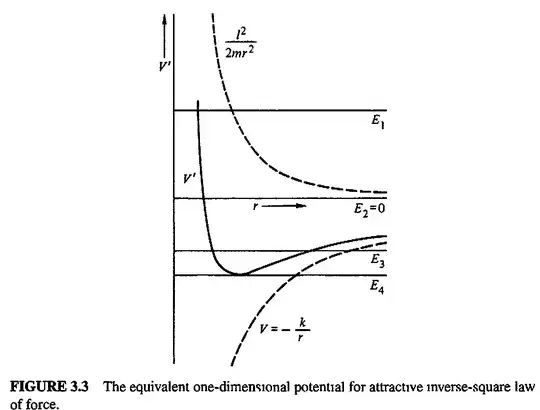
But this is not what I end up with. (I've made a Google Docs version of my spreadsheet here.)
- I start by calculating the gravitational potential at r: $V(r)=-\frac{GM_E}{r}$.
- Then multiply by the mass of the Moon to get the gravitational term (i.e. $U(r)=-\frac{GM_EM_M}{r}$).
- Then calculate the gravitational force with $F=G\frac{M_E M_M}{r^2}$ and calculate the orbital velocity with $v=\sqrt{\frac{Fr}{M_M}}$.
- Calculate angular momentum with $L = M_Mvr$.
- Calculate the value of $\frac{L^2}{2\mu r^2}$ where $\mu$ is the reduced mass $\mu = \frac{M_M M_E}{M_M+M_E}$.
- Find the resultant $\frac{L^2}{2\mu r^2} - \frac{GM_E}{r}$.
I'm making an obvious mistake somewhere, as I end up with a negative effective potential at all radii. I can't post an image because I don't have enough reputation for more than two links, but it's in the Google Docs spreadsheet linked above.