You're thinking as if $V(r)$ and $V_{\text{eff}}(r)$ were two completely different things. There is no "we can rewrite $E = T+V $ as $E = T_{\text{eff}}+V_{\text{eff}}$". They're the same thing! To see this, let us consider a system with two degrees of freedom under the action of a central-force potential.
When working in a two degrees of freedom kind of motion, we can describe the movement of an object via two coordinates (for example), $x$ and $y$. So the total kinetic energy in cartesian coordinates would read:
$$K = \frac{1}{2}m(\dot{x}^2+\dot{y}^2) $$
However, if we switch the more suited polar coordinates we can actually see the true nature of our kinetic energy. Making the substitutions $x = r\cos{\theta}$ and $y = r\sin{\theta}$ and differentiating with respect to time both $r$ and $\theta$ we get for the kinetic energy:
$$K = \frac{1}{2}m (\dot{r}^2+ r^2\dot{\theta}^2) $$
If we now look at the total kinetic energy in cartesian coordinates, we can see that:
$$E = \frac{1}{2}m(\dot{x}^2+\dot{y}^2) + V(r) \qquad \qquad \qquad(1)$$
Then again, we can reveal the true nature of our energy if we work in polar coordinates, which are more suited to our problem in hand, which leads us to:
$$E = \frac{1}{2}m (\dot{r}^2+ r^2\dot{\theta}^2) + V(r) \qquad \qquad \qquad (2)$$
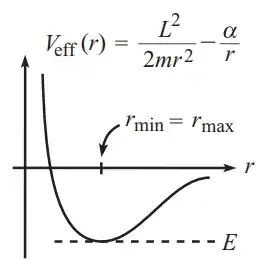
Let us remind ourselves that expressions $(1)$ and $(2)$ are completely equivalent, for all we did was a change of coordinates. If we group the potential term with the $\dot{\theta}^2$ term and using conservation of angular momentum to get rid of $\dot{\theta}$ we get the effective potential, defined as:
$$V_{\text{eff}}(r) = \frac{L^2}{2mr^2}+V(r) $$
Now you can think of your Newton equations of motion as two completely equivalent equations of motion. One for both $r$ and $\theta$, and one for specificaly $r$ alone. From Newton's second law:
$$\vec{F} = \frac{d\vec{p}}{dt} $$
Where $\vec{F} = (F_{x}, F_{y})$ and $\vec{p}= (p_{x},p_{y})$.
Working the derivatives out and working with the equations for both coordinates you can see that the equations of motion are:
$$\begin{align*} m\ddot{r} &= mr\dot{\theta}^2 -V(r) \\ \frac{d}{dt}(mr^2\dot{\theta}) &= 0\end{align*}$$
We can now make use of the effective potential in the first equation to have a one dimensional problem for $r$, as we get rid of $\theta$ thanks to conservation of angular momentum. This yields at last:
$$m\ddot{r} = \frac{L^2}{mr^3} - V(r) = -\frac{dV_{\text{eff}}}{dr} $$
Which explains why the effective potential is useful. It allowed us to get a one dimensional problem for $r$, as opposed to a two dimensional problem when considering both $r$ and $\theta$. This also reveals the true nature of the equation of motion for $r$, as we now have used all the information that was available to us.
"So someone can look at the normal potential and claim (1) as you get closer, there is an attractive force, and someone else can look at the effective potential and claim (2) as you get closer, there is a repulsive force. So who is right?". Not quite, there are not two points of view of the problem ($E = T+V$ and $E
= T_{\text{eff}} + V_{\text{eff}}$). They're the exact same point of view, and must always be considered when dealing with a central forces problem, otherwise we wouldn't be working with all the information that's available to us for the energy of the system. (1) isn't getting the whole picture of how energy has to balance itself out in order to be a constant of motion. On the other hand, remember that there are two equations of motion, one for each coordinate. This would explain why (2) is correct in this case: they're using all the information that's available to them for the problem, while (1) is not.
As for the repulsive angular momentum, remember the system has constant angular momentum. So for $L = mr^2\dot{\theta}$ as $r$ gets closer to $0$, $\dot{\theta}$ would have to grow bigger in order to keep $L$ as constant of motion, which would explain the repulsive nature of this potential.