1

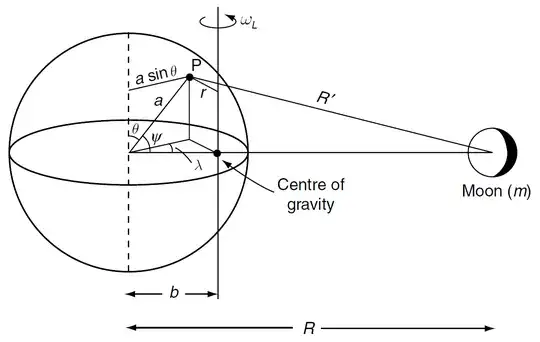
In "Physics of the Earth" by Frank Stacey and Paul Davis, they approximate the height of the tides on page 103.

They assume the Earth is perfectly spherical, covered in a uniform layer of water and that the Earth spins as fast as the Moon orbits around it, so as to present a constant face to the Moon. They use the below diagram to help with the upcoming derivation:

Figure 1

Now, they claim that the potential $W$ (their choice of variable, not mine) at the point $P$ is the sum of the potential due to the Moon's gravitational force at point $P$ and the Earth-Moon system's orbital motion about its barycentre. They state the following expression for $W$: $$W = -\frac{Gm}{R'} \color{red}{-} \frac{1}{2}\omega_L^2 r^2.\tag{1}$$

Could someone explain to me why the potential due to the orbital motion is negative? I did the following working to find it myself:

A point-like test mass at $P$ with mass $M$ would have total mechanical energy $$E = E_K + E_{rot} + E_{moon} = E_K + \frac{1}{2}I\omega_L^2 - \frac{GmM}{R'}.\tag{2}$$

Thus, $$E_K = E - \left(\frac{1}{2}I\omega_L^2 - \frac{GmM}{R'}\right).\tag{3}$$

I can call the right-hand expression the 'effective potential energy' of the system, which means that potential $W$ is $$W = \frac{U_{eff}}{M} = -\frac{Gm}{R'} \color{red}{+} \frac{1}{2}\omega_L^2 r^2.\tag{4}$$

As you can see, my 'rotational potential' is positive, as opposed to their negative value. Could someone please explain what I did wrong (or if their expression is a typo)?

Qmechanic
  • 220,844
Borealis
  • 189

3 Answers3

2

lets look at the reduce "two body" equations at the center of mass coordinate

I ) non rotate CM coordinate system

with

$$T=\frac{\mu}{2}\,\dot r^2\\ U=-\frac{G\,m\,M}{r}$$ and the Lagrange $~L=T-U~$ you obtain the EOM

$$ \mu\,\ddot r=\underbrace{-\frac{G\,m\,M}{r^2}}_{F_G}\quad\Rightarrow\\ U=-\int F_G\,dr$$

II ) rotate CM coordinate system

if the CM coordinate system rotate you obtain additional fictitious forces . the EOM is now

$$ \mu\,\ddot r=\underbrace{~-\frac{G\,m\,M}{r^2}~}_{F_G}\underbrace{~+\mu\omega^2\,r~}_{F_Z}\,\quad\Rightarrow\\ U=-\int (F_G+F_Z)\,dr=-\frac{G\,m\,M}{r}-\frac{\mu}{2}\,\omega^2\,r^2$$

so your potential energy is not correct !!

the EOM with EL

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot r}\right)=\left(\frac{\partial L}{\partial r}\right)$$

Edit:

$$\vec F_Z=-m\,(\vec\omega\times\,(\vec\omega\times \vec R))$$

with

$$\vec\omega=\begin{bmatrix} 0 \\ 0 \\ \Omega \\ \end{bmatrix}\quad, \vec R=\begin{bmatrix} r \\ 0 \\ 0 \\ \end{bmatrix}\\ \vec F_Z= \begin{bmatrix} m\,\Omega^2\,r \\ 0 \\ 0 \\ \end{bmatrix}$$

Eli
  • 13,829
2

The centrifugal force is known to be $$\vec{F}_\text{centrifugal} = M\ \omega_L^2 r\ \vec{e}_r$$ where $r$ is the distance from the axis of rotation and $\vec{e}_r$ is the unit vector pointing away from the axis.

A force (both gravitational, and centrifugal as well) is defined by the negative gradient of a potential. $$\vec{F}=-M\ \vec{\nabla}\ W$$

So with the centrifugal force from above we have $$\vec{F}_\text{centrifugal}=-M\ \vec{\nabla}\ W_\text{centrifugal}$$ or $$M\ \omega_L^2 r\ \vec{e}_r=-M\ \vec{\nabla}\ W_\text{centrifugal}$$

The solution of this equation is $$W_\text{centrifugal} = - \frac{1}{2}\omega_L^2 r^2$$ because $\vec{\nabla}(\frac{1}{2}r^2)=r\ \vec{e}_r$.

Thomas Fritsch
  • 42,352
1

I haven't done Lagrangians or Hamiltonians yet, so I didn't actually understand much of the mathematics of the posts, but these two questions answered mine as well:

Lagrangian of an effective potential

Effective potential of a two-body system

Borealis
  • 189