If you could travel to the center of the Earth (or any planet), would you be weightless there?
5 Answers
Correct. If you split the earth up into spherical shells, then the gravity from the shells "above" you cancels out, and you only feel the shells "below" you. When you are in the middle there is nothing "below" you.
Refrence from Wikipedia Gauss & Shell Theorem.
{I am using some simplistic terms, but I don't want to break out surface integrals and radial flux equations}
Edit: Although the inside of the shell will have zero gravity classically, it will also have non zero gravity relativistically. At the perfect center the forces may balance out, yielding an unstable solution, meaning that a small perturbation in position will result in forces that exaggerate this perturbation.
- 40,139
The simplest way to think about it is that there is mass all around you in the center of the Earth so you get an equal gravitational "pull" from all directions. The pulls cancel out so you get no acceleration.
If one assumes constant density for the Earth (which isn't strictly speaking true but it is close enough for this illustration) the gravitational acceleration drops linearly from 1g at the surface to 0 at the center of the Earth. So you'd get a zero if you stepped on a scale at the center of the Earth.
The more complicated explanation is that acceleration due to gravity is the derivative of the gravitational potential. This potential is a minimum at the center of the Earth and grows quadratically up to the surface. It then continues to increase at a lower rate. Since at the exact center is flat (like the bottom of a valley), the derivative which is a measure of the rate of change is zero, and there is no acceleration.
Interestingly, even though you would be weightless there, the effects of gravity are highest at the center of the Earth. You get more gravitational time dilation, for example, than you do at the surface.
I like answers that appeal to symmetry, so I answer this one with a question: If you were at the center, which way would you fall? That tells us you could stay floating there.
- 555
In the following the term "charge" refers either to mass or to electric charge and the term "Inverse Square Law" refers either to Newton's Gravitational Law or to Coulomb's Law, respectively.
SECTION 1
A. The Inverse Square Law for Spheres with uniform surface charge density
Proposition A: Let a sphere of radius $\:\rm{R}\:$ with uniform surface charge density $\:\rho_{s}\:$ and empty interior. Then:
(a1) the force exerted upon a point charge $\:\xi\:$ in the interior or on the surface of the sphere, as in Fig. 01, is zero (cancels out). In terms of potentials, the whole sphere (surface + interior) is an equi-potential region.
(a2) the force exerted upon a point charge $\:\xi\:$ in the exterior of the sphere, as in Fig. 03, is equal to the force exerted by a point particle at the center of the sphere with charge equal to its total surface charge $\:\Xi_{s}=\rho_{s}\cdot4\pi{\rm{R}}^{2}\:$. In terms of potentials, the potential outside the sphere equals that created by its total surface charge $\:\Xi_{s}\:$ concentrated on its center.
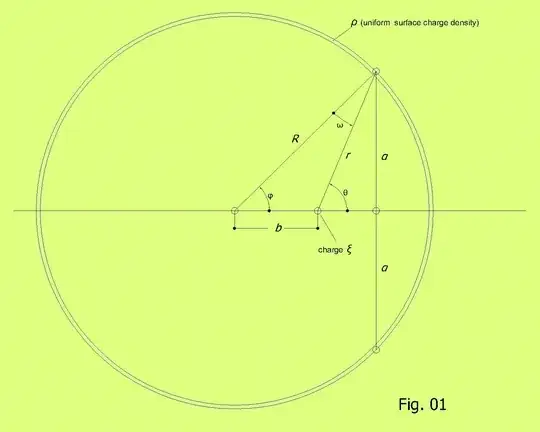
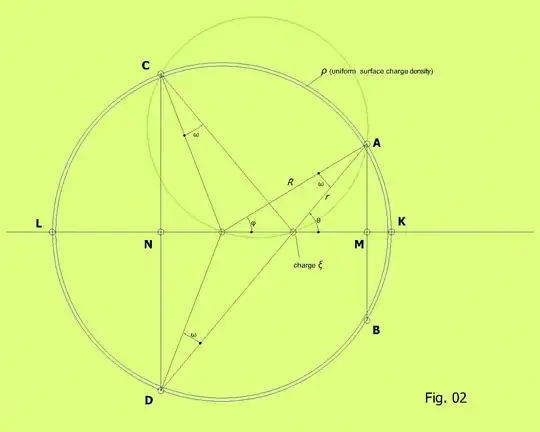
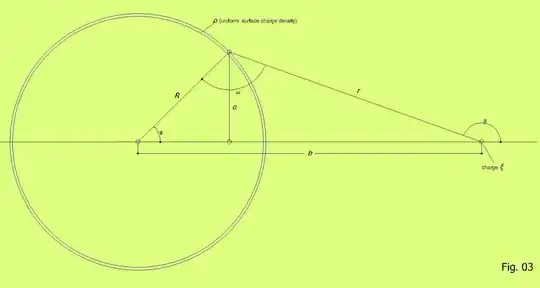
An intermediate conclusion in the proof of this Proposition is that the magnitude of the force exerted by the "cup" AKBMA of the sphere on the point charge $\:\xi\:$ in Fig. 02 is proportional to $\:\sin^{2}\omega\:$, where $\:\omega\:$ is the angle by which any point of the cyclic edge AMBA of the cup observes the line segment $\:b\:$ (that between the charge $\:\xi\:$ and the center of the sphere). More exactly this force is by magnitude:
\begin{equation} \vert \mathbf{f}_{AKBMA}\vert=k \cdot \dfrac{\Xi_{s}\cdot \xi}{{\rm{b}}^{2}}\sin^{2}\left(\dfrac{\omega}{2}\right)=\left(k \cdot \dfrac{4\pi\rho_{s}\xi{\rm{R}}^{2}}{{\rm{b}}^{2}}\right)\sin^{2}\left(\dfrac{\omega}{2}\right)=constant\cdot \sin^{2}\left(\dfrac{\omega}{2}\right) \tag{A-01} \end{equation}
But this force is cancelled by the force exerted by the "cup" CLDNC of the sphere which is equal in magnitude, but opposite direction:
\begin{equation} \mathbf{f}_{CLDNC}=\;-\;\mathbf{f}_{AKBMA} \tag{A-02} \end{equation}
So, if we remove these two "cups" the force doesn't change. But if we enlarge "cup" AKBMA by moving its cyclic edge AMBA to the left, this last will coincide with the cyclic edge CNDC of the left cup CLDNC. Then removing the two cups is as if we remove the whole sphere leaving the net force unchanged, that is, zero.
Also in Fig. 02 we have
\begin{equation} \mathbf{f}_{AMBDNCA}=\;\mathbf{0} \tag{A-03} \end{equation}
B. The Inverse Square Law for Spheres with uniform volume charge density
Proposition B: Let a sphere of radius $\:\rm{R}\:$ with uniform volume charge density $\:\rho_{v}\:$. Then:
(b1) the force exerted upon a point charge $\:\xi\:$ in the interior of the sphere located at a radial distance $\:\rm{r}\:$ from is center is equal, according to Proposition A, to that exerted by the volume charge density of a sphere of radius $\:\rm{r}\:$, $\:\Xi_{v}\left(\rm{r}\right)=\rho_{v}\cdot \dfrac{4}{3}\pi{\rm{r}}^{3}\:$, concentrated on the center. The magnitude of this force is:
\begin{equation} \vert f_{inside} \vert =k \cdot \dfrac{\Xi_{v}\left(\rm{r}\right)\cdot \xi}{{\rm{r}}^{2}}=k \cdot \dfrac{\rho_{v}4\pi\xi{\rm{r}}^{3}}{3{\rm{r}}^{2}}=constant \cdot \rm{r}\:,\quad \rm{r}\le \rm{R} \tag{B-01} \end{equation}
(b2) the force exerted upon a point charge $\:\xi\:$ in the exterior of the sphere and at radial distance $\:\rm{r}\:$ from is center is equal, according to Proposition A, to that exerted by the volume charge density of a sphere of radius $\:\rm{R}\:$, $\:\Xi_{v}\left(\rm{R}\right)=\rho_{v}\cdot \dfrac{4}{3}\pi{\rm{R}}^{3}\:$, concentrated on the center. The magnitude of this force is:
\begin{equation} \vert f_{outside} \vert =k \cdot \dfrac{\Xi_{v}\left(\rm{R}\right)\cdot \xi}{{\rm{r}}^{2}}=k \cdot \dfrac{\rho_{v}4\pi\xi{\rm{R}}^{3}}{3{\rm{r}}^{2}}=constant \cdot \rm{r}^{-2}\:,\quad \rm{r}>\rm{R} \tag{B-02} \end{equation}
SECTION 2
Suppose that Earth is a perfect sphere with uniform volume mass density. Then:
Proposition C:
(c1) A body located at the center of the Earth is weightless.
(c2) Imagine a tunnel of small cross section running along a whole diameter, so passing through the center of the Earth. A body placed in the tunnel at a radial distance $\:{\rm{r}}_{0}\:$ from the center will execute a simple rectilinear harmonic oscillation with center the center of the Earth, since in the case of gravity the force is always attractive to the center and according to equation (B-01) proportional in magnitude to the distance from this center of attraction.
- 2,348
You would not be weightless at the center of the Earth. In other words, the Earth does not follow a geodesic. Let me explain.
The Earth is not spherical, it is an oblate spheroid. The acceleration of a uniform non-spherical body in a spherical gravitational field does not follow an inverse square law. The acceleration of the center of mass does not equal the acceleration at the center of mass. An accelerometer fixed at the center of the Earth would read approx 1.75 pgal (1.75e-14 m/$\mathrm{s^2}$), not zero.
- 1,642