When gravity spacetime is visualized, it's a sag with the lowest point in the middle of the planet/star as you can see here:
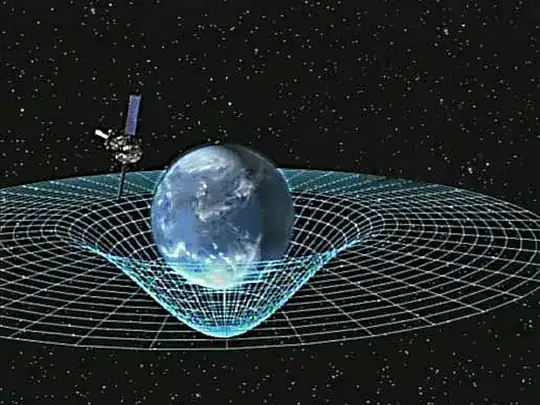
For all planets and stars, there is zero G in the core due to that the surrounding mass cancels out each other. This means that the gravity pull is strongest at the surface or close to it? Shouldn't this mean that the gravity spacetime should be visualized as a doughnut/ring instead with lots of gravitational pull at the edge, but not in the middle/core?
On one hand, the graph in OP's picture seems to represent the gravitational potential $U$ of a spherically symmetric planet, which indeed attains its minimum at $r=0$, cf. a potential well.
On the other hand, OP is presumably referring to the magnitude $|\vec{g}|$ of the gravitational field strength $\vec{g}= -\nabla U$ as being donut shaped, because $|\vec{g}|$ vanishes for $r\to 0$ and $r\to \infty$, cf. e.g. this and this Phys.SE posts. This recent Phys.SE question uses the word donut in the same sense. Topologically, the relevant shape is a hollow ball or a thick sphere $S^2\times I$; while a donut usually refers to either a solid torus $S^1\times D^2$, or its surface: the torus $S^1\times S^1$.
As I read your question, I think you are confusing the idea of the "core". The core is considered a point inside the sphere. I am assuming you are looking at the picture and possibly confusing the core as the central mass above the larger depression in the spacetime graphic representation. I don't know if that helps, because my assumption of your assumption can be wrong.
