Assume that a solid sphere with radius $b$ is charged with a volumetric charge density of $\rho$. Calculate the electric field inside and outside of the sphere.
We're expected to use Coulomb's law in this problem because our professor said we're not allowed to use Gauss for the first exam... Anyway, should I prove that, considering a point outside of the sphere ($R > b$), I can consider that all the charge is located at the center of the sphere? If so, how can I prove it?
The easiest way would probably be to use spherical coordinates and to either do this using the Coulomb force or the potential thereof, locating your field point along the $z$-axis and using symmetry to argue that the only component of the force which survives is the $\hat z = \hat r$ component.
So we have a source point at $(b,\theta,\phi)$ and a field point at $(z, 0, 0)$ and the $z$-component of the source point is $b~\cos\theta$ while the perpendicular component is $b~\sin\theta$, so the distance from the source to the field point is $$s = \sqrt{(z - b\cos\theta)^2 + b^2\sin^2\theta} = \sqrt{z^2 + b^2 - 2 z b \cos\theta}.$$
So the integral is $$V(z) = -\frac\sigma{4\pi\epsilon_0} \int_0^\pi b~d\theta\int_0^{2\pi} b~\sin\theta~d\phi\frac{1}{\sqrt{z^2 + b^2 - 2 z b \cos\theta}}.$$This actually is naturally integrated in $s$-space, where we have seen $s^2=z^2+b^2-2zb\cos\theta$ we find that we can do a substitution with $2s~ds=2zb\sin\theta~d\theta$ while $s(0) = z-b$ and $s(\pi) = z+b.$ Therefore we will find $$V(z) = -\frac\sigma{2\epsilon_0}~b^2~\int_{z-b}^{z+b}\frac{s}{zb}~ds~\frac{1}{s},$$culminating in $$V(z) = -\frac\sigma{2\epsilon_0}~b^2~\frac{2b}{zb} = -\frac{\sigma~b^2}{\epsilon_0~z}.$$Recognizing that the total charge is $Q = 4\pi~b^2~\sigma$ this can now be rewritten as $$V(z) = -\frac{Q}{4\pi\epsilon_0~z}.$$Combined with the knowledge from symmetry that the force is only in the $\hat z$-direction, the field $-\nabla V$ is just going to be the same as the Coulomb field, if that charge were concentrated at the origin.
1) Maxwell's equations state $\nabla \cdot \vec{E} = \rho $
2) The divergence theorem states that $\int \nabla \cdot \vec{E} dV = \int \vec{E} \cdot d\vec{A}$ through any closed surface for any vector field $\vec{E}$.
3) Therefore if you take a spherical shell the radius of point b, then integrate over it, you get $\int \nabla \cdot \vec{E} dV = \int \rho dV.$ But this is $\int\vec{E} \cdot d\vec{A} = Q_{enclosed}$.
4) Because $\rho$ is spherically symmetric, the electric field must also be spherically symetric (how could it possible not be?) Therefore, $\int\vec{E} \cdot d\vec{A}$ is just $\vec{E} * 4\pi b^2.$
So $\vec{E} * 4\pi b^2 = Q$
$\vec{E}(b) = \frac{Q}{4\pi b^2}$
Hints :
Although you could solve your problem by direct volume integration, I suggest to work first the problem to find the electric field inside and outside of a sphere with uniform surface charge density $\:\rho_{s}\:$. You'll end up with a very simple result for each case. Using these results you'll find the answers for a sphere with uniform volume charge density $\:\rho_{v}\:$ very easy.
(1) To find the field inside a sphere with uniform surface charge density $\:\rho_{s}\:$ : Three Figures and first steps are given below.
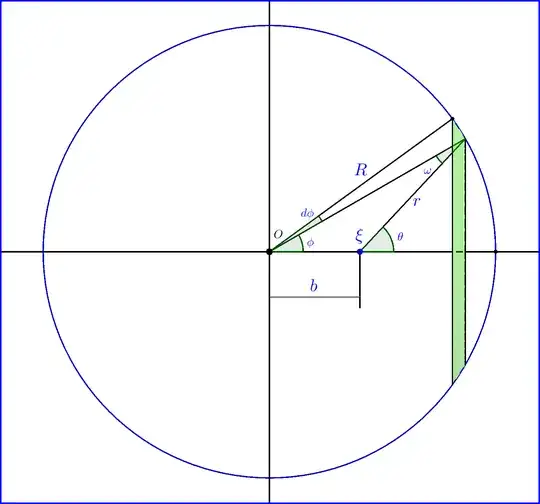
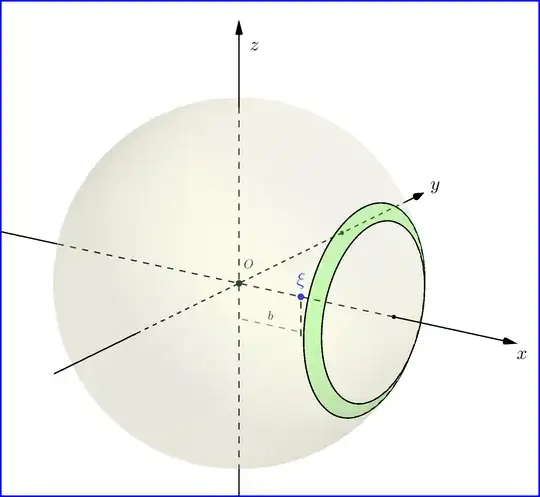
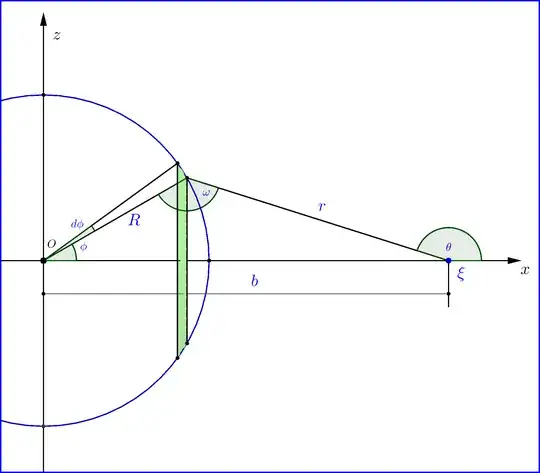
A point charge $\xi$ is located on the $x$-axis at a distance $b\left(\leq R\right)$ from the center $O$ of the sphere of radius $\:R\:$, origin of a $Oxyz$ Cartesian coordinates system. The charge of the infinitesimal ring, $\mathrm{d}\Xi_{ring}$, is
\begin{equation} \mathrm{d}\Xi_{ring}=\rho_{s}\,\mathrm{d}{\rm{S}}_{ring} \tag{01} \end{equation} where $\mathrm{dS}_{ring}$ the area of the infinitesimal ring. This ring has perimeter $2\pi R\sin\phi=2\pi\; r\sin\theta$ and width $R\,\mathrm{d}\phi$ so \begin{equation} \mathrm{dS}_{ring}=2\pi R^{2}\sin\phi\,\mathrm{d}\phi = 2\pi R\, r \sin\theta\, \mathrm{d}\phi \tag{02} \end{equation} and \begin{equation} \mathrm{d}\Xi_{ring}=2\pi \rho_{s} R^{2}\sin\phi\,\mathrm{d}\phi = 2\pi\rho_{s}R\,r \sin\theta\,\mathrm{d}\phi \tag{03} \end{equation} The force $\mathrm{dF}_{ring}$ exerted by the infinitesimal ring on the point charge $\xi$ is along the $x$-axis of absolute value \begin{equation} \mathrm{dF}_{ring}=k\cdot\dfrac{\xi\cdot \mathrm{d}\Xi_{ring} }{r^{2}}\cos\theta=\left(2\pi k \rho_{s}\xi R^{2}\right)\dfrac{\cos\theta}{r^{2}}\sin\phi \,\mathrm{d}\phi \tag{04} \end{equation}
From this point is up to you to integrate and find a very simple result.
(Don't be disappointed : although simple trigonometry, it's a difficult step.)
(2) To find the field outside a sphere with uniform surface charge density $\:\rho_{s}\:$ : One Figure is given below.
