Why is Earth's gravitational pull only at its center?
Does acceleration due to gravity remain constant wherever I go in and on the Earth?
5 Answers
If the Earth were a perfect sphere, it would be the same everywhere on Earth's surface. This is known as the shell theorem. It's not too hard to show mathematically, but you can think of it as the fact that all the mass that is close to you balances roughly with the mass that is far away. If you were to tunnel into the Earth, however, you would only experience gravity due to the mass that was closer to the center than you. The gravity you feel would go down.
In real life, the Earth is not a perfectly uniform sphere, and this is used to make gravity maps of the surface for geological surveys, etc. It is also spinning, which gives an apparent difference between gravity at the poles/equator.
- 10,247
- Why is Earth's gravitational pull only at its center?
It is not. In fact, the earth's gravitational pull is a mathematical abstraction. The Earth, as a whole, does not have a Gravitational pull. Each tiny bit of the earth, each atom, each particle, has its own individual tiny gravitational pull. What we think of as the overall gravitational pull of the earth is a mathematical result of adding up the individual contributions of each of these individual bits. We consider this resulting sum as acting at the center because it turns out that for any spherical shell of uniform density, if you add the contributions of every bit of each tiny piece of that shell, and its effect on any point inside the shell, (not just its center), they all cancel out. and for any point outside the shell, the result of adding up all the pieces turns out to be exactly the same as if all the bits and pieces were located at the center. This is a standard example problem used in Integral calculus texts/courses. In other words, if a spherical shell is hollow, there is no gravitational force inside the shell. This means that at any point inside a sphere, the total gravitational force can be calculated based only on the materiel inside the sphere that is as deep or deeper than the point in question. - Does acceleration due to gravity remain constant wherever I go in
and on the Earth?
if the Earth was exact non-rotating sphere, of uniform density, the answer to your question would be yes. But it is not. SO there are small variations in the gravitational field due to those differences. Where there is denser material below the surface, the gravitational force is slightly higher. Indeed, this effect is measured by some satellites and used to assist in detection of mineral deposits below the surface. Because of the earth's rotation, the earth is a flattened obloid, and so the distance to the center is greater at the equator than at the poles, reducing gravity slightly. Also, the centrifugal force at the equator is greater which also slightly reduces the gravitational force.
- 190
No, the Earth's gravity varies over its surface because (a) the Earth is not spherical, (b) it does not have a uniform (or spherically symmetric) distribution of density and (c) of course the "surface" is at different heights.
You can find a local gravitational strength (and direction - because the local gravitational vector does not necessarily point to the centre of the Earth) at Wolfram Alpha, using this sort of query.
You also ask about the interior gravity. If the Earth was a uniform density sphere, then it is easy to use Gauss's theorem to show that the gravitational acceleration should depend linearly with radius, decreasing to zero at the centre of the Earth. Whilst the gravity at the centre of the Earth is approximately zero (don;t forget there are lots of other sources of gravity in the universe!), the interior density profile of the Earth is not uniform. Taking this into account one can calculated an (azimuthally averaged) gravity a a function of radius insde the Earth. It looks like this: (from wikipedia).
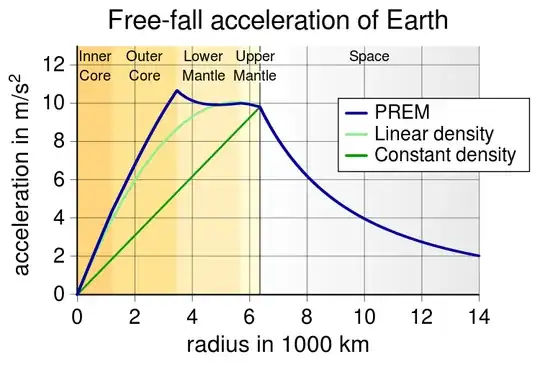
- 141,325
No, acceleration due to gravity varies, depending solely on the altitude on which Gravitational force is working, the approximate* value can be determined using equations: g(eff, h) = g*[(r/r h)^2] H being the altitude, r being earth's mean radius, g effective is the acceleration due to gravity at an altitude h above sea level. Thanks :) Approximate because : other factors like geological variations also account for, these are tracked using various satellite instruments.
- 235
No, the earth doesn't have a uniform gravitational field. This is because we know that:
height is inversely proportional to gravity or $g$,
the earth is spheroidal and not a complete sphere. You can also think of the earth as an oval of sorts. Now because of this, the poles will be closer to the earth whereas the equatorial region will be the farthest from earth.
Therefore, we can say that the gravitational field near the poles is slightly stronger than the one experienced near equatorial regions.
However, please don't misunderstand that earths rotation affects its gravitational field, because frankly it does not. The centripetal forces affects weight of the person i.e. if you calculate your weight in the equator or poles due to centripetal acting on equator the most causes apparent weight which is less than actual weight.
In this way it adheres your weight but not gravity. Gravity on earth is not uniform because of it being a non-perfect sphere and probably some other factors. But I believe it is largely due to it being spheroidal in shape.