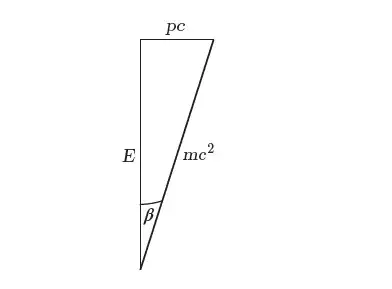
Update: It’s unfortunate that $\beta$ (Instead of $\theta$ or $\phi$ ) was chosen for the rapidity in the diagram above, since $\beta$ is traditionally the dimensionless velocity factor $v/c$ (as I use below). [I think Einstein used $\beta$ for the time-dilation factor.]
For simplicity, assume all motions occur in the $x$-direction.
Draw the [planar] energy-momentum diagram for a collision.
- For two particles before the collision,
I usually draw the sum of their 4-momenta
$\tilde m_1 + \tilde m_2$ tip-to-tail with first tail at the origin.
- ( $\tilde m_1$ is a timelike vector with [in natural units]
magnitude $m_1$ (the invariant [rest-]mass) and
rapidity $\theta_1=\mbox{arctanh}(\beta_1)$ where $\beta_1=\tanh\theta_1$ is the dimensionless-velocity,
timelike leg $E_1=m_1\cosh\theta_1 =\gamma_1 m_1$, and
spacelike leg $p_1=m_1\sinh\theta_1 = v_1\gamma_1 m_1$....
and similarly for the other 4-momenta.)
- For two particles after the collision,
then draw the sum of their 4-momenta
$\tilde m_3 + \tilde m_4$ tip-to-tail with first tail at the origin.
- For conservation,
the tip of $(\tilde m_3 + \tilde m_4)$ must coincide with the tip of
$(\tilde m_1 + \tilde m_2)$.
Now, treat this as if it were "an equilibrium problem [using a "free body diagram"]
involving 4 coplanar forces" in Newtonian mechanics....
but using hyperbolic trig-functions instead
of the ordinary Euclidean trig-functions.
Given some knowns
[among various known components, known magnitudes, or known rapidities],
find the unknowns.
You may use components, or you can use vector-methods involving dot-products.
From a post of mine
( Mass Addition in Special Relativity)
here is the diagram for a particular totally inelastic collision.
$$M=(m_1\cosh\theta_1+m_2\cosh\theta_2)=(\gamma_1 m_1 + \gamma_2 m_2).$$
Go there to see that specific problem worked out.
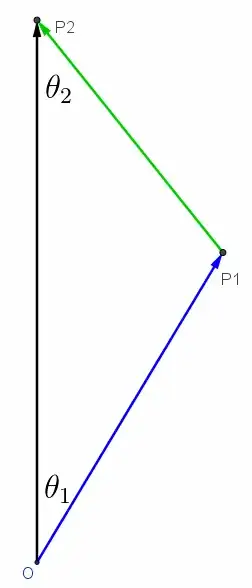
Here's are links to more complicated problems I worked out.
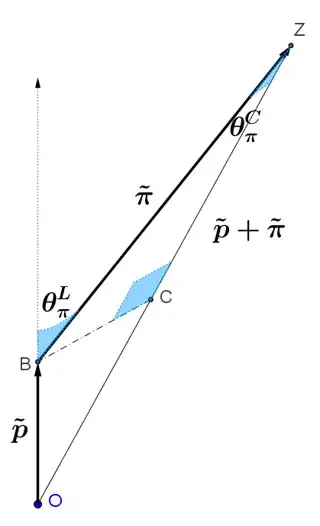
( Momentum in center of mass-frame out of knowledge kinetic energy in lab-frame )
( COM frame in Relativistic particle physics )
( How to determine particle energies in center of momentum frame? )
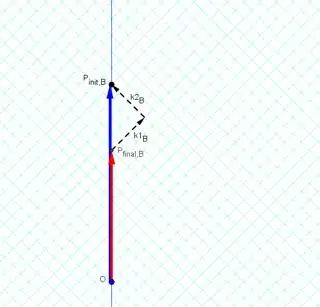
( On conservation of momentum and doppler shift in special relativity )
(For an elastic collision using a new method of mine, visit the end of
https://www.physicsforums.com/insights/relativity-rotated-graph-paper/ )
[update:
I think the reference to Tevian Dray is either
his book "The Geometry of Special Relativity" [on Amazon]
or his article "The geometry of relativity" in the American Journal of Physics 85, 683 (2017); https://doi.org/10.1119/1.4997027 .
You might be able to find drafts on his website.]