I think your formula
$$\displaystyle |\vec{p}^{\text{com}}_{\pi}|=\frac{M_{p}\sqrt{T^{L}_{\pi}(T^{L}_{\pi}+2M_{\pi})}}{\sqrt{(M_{p}+M_{\pi})^{2}+2T^{L}_{\pi} M_{p}}}$$
assumes that the target particle $P_p$ is initially at rest in the lab frame.
This condition was used in @JEB 's answer.
Here's a geometric interpretation of the formula, followed by the more general formula.
(I'll admit that it took me a while to realize this. I recall your question and the quick answer from when these were first posted. Upon its recent bump by Community, I thought about it again.)
The strategy below can be used to geometrically interpret other similar formulas.
Your formula gives the altitude (segment BC) of a triangle [representing conservation of total 4-momenta] in energy-momentum space ,
where the base (segment OZ) is the system's total momentum 4-vector (which I will write as $\tilde p + \tilde \pi$ [to declutter the formulas])
and one side (segment OB) is the target's 4-momentum $\tilde p$, which is (by assumption) initially at rest in the lab-frame $\hat L$.
(The rapidities are shown. In addition, I marked that segment BC (spatial momentum in the COM-frame) is Minkowski-perpendicular to segment OZ (the worldline of the COM-frame).
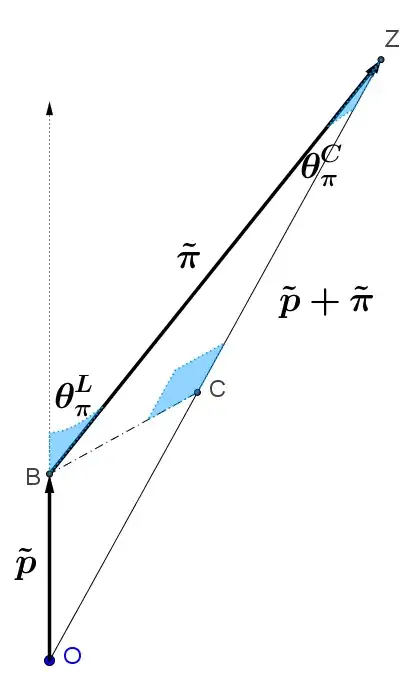
Let's write your formula using rapidities (the Minkowski-angle $\theta$ between future timelike vectors, where $\beta=\tanh\theta$ and $\gamma=\cosh\theta$). This will reveal what the numerator and denominator represent.
With rapidities, the 4-momentum $\tilde \pi$ can be expressed in terms of
- rest mass $m_{\pi}=\pi =\sqrt{\tilde \pi \cdot \tilde \pi}$,
- energy $E_{\pi}=\pi\cosh\theta=\tilde\pi\cdot\hat t$ (in a general frame $\hat t$),
- momentum $p_{\pi}=\pi\sinh\theta = \tilde\pi\cdot\hat t_{\bot}$ , and
- kinetic energy $T_{\pi}=\pi (\cosh\theta -1)$
So, your formula
$$\displaystyle |\vec{p}^{\text{com}}_{\pi}|=\frac{M_{p}\sqrt{T^{L}_{\pi}(T^{L}_{\pi}+2M_{\pi})}}{\sqrt{(M_{p}+M_{\pi})^{2}+2T^{L}_{\pi} M_{p}}}$$
becomes... (where I will manipulate the numerator and denominator separately)
\begin{align}
|\pi\sinh\theta^C| &=
\frac{
p\sqrt{\pi(\cosh\theta^L-1) (\pi(\cosh\theta^L-1)+2\pi)}
}
{
\sqrt{
(p+\pi)^2+2\pi(\cosh\theta^L-1)p
}
}
\\
&=
\frac{
p\sqrt{\pi(\cosh\theta^L-1) \pi(\cosh\theta^L+1)}
}
{
\sqrt{
(p^2+\pi^2+2p\pi) + 2\pi\cosh\theta^L-2\pi p
}
}
\\
&=
\frac{
p\pi \sqrt{\sinh^2\theta^L}
}
{
\sqrt{
p^2+\pi^2+ 2\pi\cosh\theta^L
}
}
\end{align}
Since (by assumption) $\tilde p$ is at rest in the lab-frame $\hat L$,
the rapidity-with-respect-to-the-lab $\theta^L$ is equal to the rapidity between the 4-momenta $\tilde \pi$ and $\tilde p$:
\begin{align}
|\pi\sinh\theta^C|
&=
\frac{
p\pi \sqrt{\sinh^2\theta_{between\ \pi\ and\ p}}
}
{
\sqrt{
p^2+\pi^2+ 2\pi\cosh\theta_{between\ \pi\ and\ p}
}
}
\\
&=
\frac{
p\pi \sinh\theta_{between}
}
{
\sqrt{
(\tilde p + \tilde \pi)\cdot(\tilde p + \tilde \pi)
}
}
\\
&=
\frac{
p\pi \sinh\theta_{between}
}
{
|\tilde p + \tilde \pi|
}
=
\frac{| \tilde p \times \tilde \pi |}{ | \tilde p + \tilde \pi | }
\\
&=
\frac{
\mbox{area of parallelogram [or kite] with sides $\tilde p$ and $\tilde \pi$}
}
{
\mbox{diagonal of parallelogram [or kite] with sides $\tilde p$ and $\tilde \pi$}
}\\
&=
\frac{
\mbox{2(area of triangle with sides $\tilde p$ and $\tilde \pi$)}
}
{
\mbox{base of triangle with sides $\tilde p$ and $\tilde \pi$}
}\\
&=
(\mbox{altitude of triangle with sides $\tilde p$ and $\tilde \pi$ })
\end{align}
So, the more general relation is
$$\displaystyle |\vec{p}^{\text{com}}_{\pi}|=\frac{M_{p}\sqrt{T^{p}_{\pi}(T^{p}_{\pi}+2M_{\pi})}}{\sqrt{(M_{p}+M_{\pi})^{2}+2T^{p}_{\pi} M_{p}}}$$
which involves " the kinetic energy of $\tilde \pi$ in the frame of $\tilde p$ ''.
If your target $\tilde p$ is not at rest in the lab-frame $\hat L$,
then you can substitute
$$\theta_{\pi p}=\theta_{\pi L} - \theta_{p L},$$
expand out using hyperbolic-trig-identities and translate into masses, energies, and momenta.
Then your expression will become more complicated, involving components of $\tilde p$ in the lab-frame.
If you take the calculation with rapidities a little further (and I'll make the $\pi$ explicit in $\theta_{\pi}^C$ and drop the magnitude on the left),
one gets The Law of Sines in Minkowski-spacetime:
\begin{align}
\pi \sinh\theta_\pi^C
&=
\frac{
p\pi \sinh\theta_{between}
}
{
|\tilde p + \tilde \pi|
}\\
\sinh\theta_\pi^C
&=
\frac{
p \sinh\theta_{between}
}
{
|\tilde p + \tilde \pi|
}\\
\frac{\sinh\theta_\pi^C}{p}
&=
\frac{
\sinh\theta_{between}
}
{
|\tilde p + \tilde \pi|
} = \frac{\sinh\theta_p^C}{\pi}
\end{align}
where $\theta_\pi^C$ is the Minkowski-angle opposite to $\tilde p$
and $\theta_{between}$ is the external Minkowski-angle at the vertex B opposite to $\tilde p + \tilde \pi$,
and, by symmetry,
$\theta_p^C$ is the Minkowski-angle opposite to $\tilde \pi$.
(We can't use the "internal angle" at B because that would be a Minkowski-angle
between a future-timelike and past-timelike vector.
No arc of a hyperbola is cut by those vectors.
With some work, one might be able to define such a thing.)
