On conservation of momentum and doppler shift in special relativity

Question

If a particle emits two equal frequency light rays, its momentum is conserved. But the particle has an apparent momentum change in a moving frame due to doppler shift. How can one distinguish between these two frames.

Answer 1

Here's an energy-momentum diagram supporting @Dale's answer.
The rotated graph paper helps one see Doppler factors involved.

The diagram is from an old answer of mine to Momentum conservation with photons

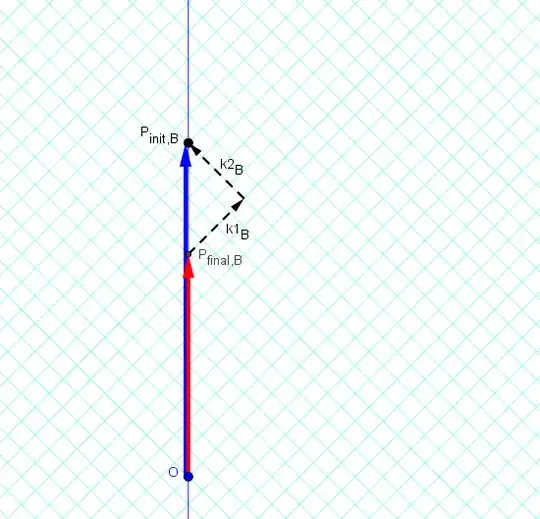
Conservation of total 4-momentum for the emission of two photons is $$\tilde P_{fin}+\tilde {k_1}+\tilde {k_2}=\tilde P_{init}$$

In the emitter frame [the B-frame], we have emitted photons with equal frequency (equal energies)

In the lab frame [the A-frame] (in which the particle has velocity (3/5)c), we have emitted photons with unequal frequencies (unequal energies), with Doppler factor k=2:

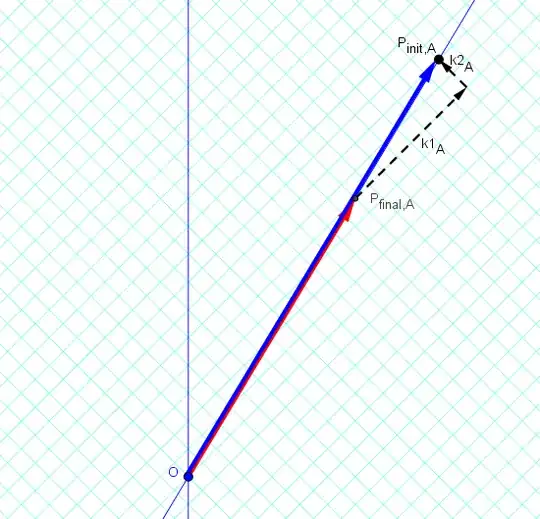
In both cases, the emitting particle has its [rest-]mass decreased (of course, by the same amount).

Answer 2

If a particle emits two equal frequency light rays , it's momentum is conserved.But the particle has an apparent momentum change in a moving frame due to doppler shift.

As you say, in a reference frame where the particle is moving the forward light is blue shifted and the rearward light is red shifted. Since the momentum of the light is proportional to its frequency, that implies that more momentum is carried forward than is carried backwards.

Conservation of momentum therefore requires that the momentum of the particle decrease. The velocity of the particle is not changed, therefore it is the mass of the particle which must reduce to account for the diminished momentum.

Both the four-momentum and the three-momentum of the total system are conserved. For example, using units where $c=1$, suppose that we start with a particle of mass 10 eV at rest which then emits a pair of 1 eV photons, one along the positive x axis and the other along the negative x axis.

So the initial four momentum of the particle is $(10,0,0,0)$ and the four momenta of the final particle and the two photons are respectively $(8,0,0,0)$, $(1,1,0,0)$, and $(1,-1,0,0)$. Note that the mass of the particle has decreased from 10 eV to 8 eV. Transforming to a frame where the particle is moving at 0.6 c in the x direction we get an initial four momentum of $(12.5,7.5,0,0)$ and a four momentum of $(10,6,0,0)$ and $(2,2,0,0)$ and $(0.5,-0.5,0,0)$ for the final particle and the two photons. Note that momentum and energy are conserved in both frames and that the mass of the particle has again decreased from 10 eV to 8 eV. Also, since $v=p/E$ you can see that the velocity of the final particle remains 0.6 c.