How to determine particle energies in center of momentum frame?

Question

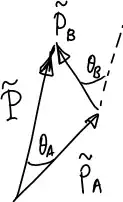
I want to show for the following process that, except for the angle $\theta$, all momenta and energies are fixed by energy-momentum conservation. 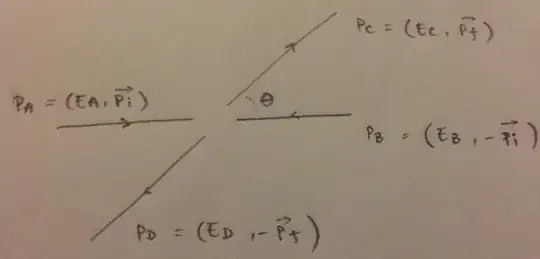Namely: $$p_A=\frac{1}{2\sqrt{s}}(s+m^2_A-m^2_B\space,\space 0\space,\space 0\space,\space\sqrt{\eta_i})$$ $$p_B=\frac{1}{2\sqrt{s}}(s-m^2_A+m^2_B\space,\space 0\space,\space 0\space,\space -\sqrt{\eta_i})$$ $$p_C=\frac{1}{2\sqrt{s}}(s+m^2_C-m^2_D\space,\space \sqrt{n_f}sin(\theta)\space,\space 0\space,\space\sqrt{n_f}cos(\theta))$$ $$p_D=\frac{1}{2\sqrt{s}}(s-m^2_C+m^2_D\space,\space -\sqrt{n_f}sin(\theta)\space,\space 0\space,\space-\sqrt{n_f}cos(\theta))$$

, where $\eta_i=4s|\vec{p_i}|^2$ and $\eta_f=4s|\vec{p_f}|^2$. That said, my approach was to determine the energies and 3-momenta at the center of momentum reference frame for each particle, with a fixed $s$, and check it corresponds to each one of the above, but I'm having some trouble proving that, for example, $E_A=\frac{s+m^2_A-m^2_B}{2\sqrt{s}}$. I've been playing around with $(p_A+p_B)^2=(E_A+E_B)^2=s$ but i'm failing to determine $E_A$. How should I do it?

Answer 1

The center of momentum frame has 4-velocity given by $\hat P$, where $\tilde P=\tilde p_A+\tilde p_B$ and $\hat P=\frac{\tilde P}{\sqrt{\tilde P\cdot \tilde P}}$.
The energy of particle A in that frame is therefore $E_{A,COM}=\tilde p_A \cdot \hat P$.

From your given, $\tilde P=\frac{1}{2\sqrt{s}}(2s,0,0,0)=(\sqrt{s},0,0,0)$. (So, $s=\tilde P\cdot\tilde P$.)
Thus, $\hat P=(1,0,0,0)$. So, it looks like you have given components in the COM-frame. (So, I see now that your goal is to obtain these given expressions.)

Using an energy momentum diagram, $\tilde P=\tilde p_A+\tilde p_B$, where my $\theta_A$ and $\theta_B$ are rapidities (where $v_A=\tanh\theta_A$ is the spatial velocity in this frame—- my $\theta$’s are not spatial angles in the OP’s diagram).

To find $E_{A,COM}=\hat P \cdot \tilde p_A$, note that $\tilde P=\tilde p_A+\tilde p_B$ implies (since we care least about B) $$\tilde p_B=\tilde P-\tilde p_A$$ and thus (essentially the Minkowski analogue of the Law of Cosines) \begin{align} \tilde p_B \cdot \tilde p_B &=\tilde P\cdot\tilde P +\tilde p_A\cdot\tilde p_A -2\tilde P\cdot \tilde p_A\\ m_B^2 &=s+m_A^2-2(\sqrt{\tilde P\cdot \tilde P}\hat P)\cdot \tilde p_A\\ &=s+m_A^2-2\sqrt{s}(\hat P\cdot \tilde p_A)\\ m_B^2&=s+m_A^2-2\sqrt{s}(E_{A,COM})\\ \end{align} and you're done.