(The problem in the OP appears to be from Rindler, Relativity: Special, General, and Cosmological, 2ed, Exercise 6.7.)
The statement
"in the CM [zero-momentum, center of momentum] frame $(P'-Q)$ has no spatial components" means that $(P'-Q)$ is parallel to the total-4-momentum $(P+Q)$, also $(P'+Q')$ [by conservation]. This appears to hold true when the collision is elastic.
As I was writing this, I eventually arrived at a simpler solution in the end.
But I've kept what I started with because it may be useful to others (as it was to me).
Inspired by the Mandelstam variables
( https://en.wikipedia.org/wiki/Mandelstam_variables )
(which I am learning more about)
I can prove it using dot-products... but can't easily explain it in those terms... but I suspect there is a simpler method using dot-products using the 4-momenta directly... when things get sorted out.
In these terms, let me define the following 4-vectors:
$S=P+Q=P'+Q'$ (the total-4-momentum) ,
$T=P-P'=Q'-Q$, (the 4-momentum transfer) and
$U=P-Q'=P'-Q$ (some kind of cross term),
where I have used momentum conservation ($P+Q=P'+Q'$) to write the second equality in each.
It's easy to show that $S\cdot T=0$ (the momentum-transfer is orthogonal to the total-momentum).
What you want to show is that,
for elastic collisions,
$U$ is parallel to $S$ by showing that $U\cdot T=0$.
(By elastic, we have, in addition to $P+Q=P'+Q'$,
the conditions $P^2=P'^2$ and $Q^2=Q'^2$.)
First note that $$S^2=(P+Q)^2=P^2+2P\cdot Q+Q^2.$$
Next, note that $$S+T+U=(3P+Q-P'-Q')=2P,$$
where I invoked momentum conservation.
It can be shown that $S^2+T^2+U^2=P^2+Q^2+P'^2+Q'^2$, which equals $2(P^2+Q^2)$ in the elastic case.
By squaring $T+U=2P-S=P-Q$ and isolating $2T\cdot U$,
I get
$$\begin{align}
2 T\cdot U
&=P^2-2P\cdot Q+Q^2 -[T^2+U^2]\\
&=P^2-2P\cdot Q+Q^2 -[2(P^2+Q^2)-S^2]\\
&=-P^2-2P\cdot Q-Q^2 +S^2\\
&=0
\end{align}
$$
There's likely a simpler calculation with dot-products [without invoking Mandelstam] which might be suggested by the following energy-momentum diagram. (update: there is)
Now here's an energy-momentum diagram, which suggests a simpler geometric interpretation.
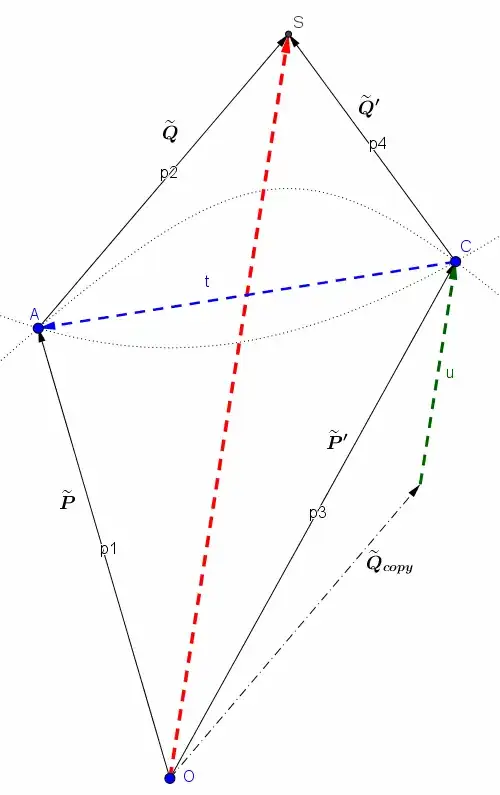
The 4-vector $U=P'-Q=P'-Q_{copy}$ is shown, connecting the tip of $Q_{copy}$ to $P'$.
The momentum-transfer segment $T$ (connecting A and C), which is orthogonal to the total-momentum $S$, is actually bisected by $S$ when the collision is elastic... that is when $C$ (the tip of $P'$ and the tail of $Q'$) is at the intersection of the two mass-shells determined by $P$ and $Q$.
So, this means that in the zero-momentum COM frame,
the spatial part of $Q$ (which is projected onto half of $T$) is equal to the spatial part of $P'$ (which is projected onto the other half of $T$). Thus, the difference in their spatial components is zero.
Thus, $U\cdot T=(P'-Q)\cdot T=P'\cdot T - Q\cdot T=P'_{x,COM}-Q_{x,COM}=0$.
Okay, after writing this up and thinking about it some more...
Here is a simpler calculation. (I'll leave the earlier stuff up there because it may be useful. It was to me.)
$$\begin{align}
0&\stackrel{?}{=}U\cdot T\\
&=(P'-Q)\cdot T\\
&=(P'-[P'+Q'-P])\cdot T \qquad \mbox{invoking conservation}\\
&=(P'+P-[P'+Q'])\cdot T\\
&=(P'+P)\cdot T-[P'+Q']\cdot T\\
&=(P'+P)\cdot T- \qquad 0\qquad\quad \mbox{since $S\cdot T=0$}\\
&=(P'+P)\cdot (P-P')\\
&=P'^2-P^2\\
&=\qquad 0 \qquad \qquad \qquad\qquad \mbox{since $P'^2=P^2$ for an elastic collision}\\
\end{align}
$$
One more update.
I think the following variant of the last calculation constructs $U$ as a multiple of $S$:
$$\begin{align}
U&=(P'-Q)\\
&=(P'-[P'+Q'-P])\qquad \mbox{invoking conservation}\\
&=(P'+P-[P'+Q'])\\
&=(P'+P)-[P'+Q']\\
&=(P'+P) -S\qquad\qquad\quad \mbox{since $S=P'+Q'$}\\
\end{align}
$$
Since $P'$ and $P$ are future-pointing timelike, then so is $(P'+P)$.
For an elastic collision $(P'+P)$ is a multiple of $S$, because of symmetry [recall $P^2=P'^2$ for an elastic collision]... and it seems we need that $P$,
$P'$, and $S$ are coplanar.
From the diagram, $(P'+P)$ has magnitude $2P\cosh\theta_{PS}$, where $\theta$ is the rapidity between $P$ and $S$.
So, it seems (assuming no errors in the calculation and the diagram)
that since $S$ has magnitude $P\cosh\theta_{PS}+Q\cosh\theta_{QS}$,
then, for an elastic collision [with $P$, $P'$,and $S$ coplanar],
$U$ is a multiple of $S$ and
$U$ has magnitude $| P\cosh\theta_{PS}-Q\cosh\theta_{QS}|$,
the difference of the relativistic-energies-in-the-COM-frame.
