Is this symmetry factor in Peskin wrong?

Question

I am trying to compute the symmetry factor of a Feynman diagram in $\phi^4$ but i do not get the result Peskin Claims. This is the diagram I am considering

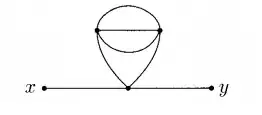
$$\left(\frac{1}{4!}\right)^3\phi(x)\phi(y)\int{}d^4z\,\phi\phi\phi\phi\int{}d^4w\,\phi\phi\phi\phi\int{}d^4v\,\phi\phi\phi\phi$$

my attempt is the following: there are 4 ways to join $\phi(x)$ with $\phi(z)$. There are then 3 ways to connect $\phi(y)$ with $\phi(z)$. Then, there are 8 ways to connect $\phi(z)$ with $\phi(w)$ and 4 ways to contract the remainning $\phi(w)$ with $\phi(v)$. Finally the there are 6 ways to contract the $\phi(w)$ and the three $\phi(v)$ in pairs

$$\left(\frac{1}{4!}\right)^3\dot{}4\dot{}3\dot{}8\dot{}4\dot{}6=\frac{1}{6}$$

but the result claimed in Peskin (page 93) is $1/12$. What am I doing wrong?

Answer 1

What am I doing wrong?

The expansion of $e^x$ is: $$ e^x=1+x+x^2/2+x^3/3!+\ldots $$

From expanding the expression: $$ \left<\phi_x\phi_y\exp{\left(-\frac{\lambda}{4!}\int dz \phi_z^4\right)}\right>\;, $$ the third order term is: $$ \left< \phi_x\phi_y\frac{1}{3!}{\left(\frac{-\lambda}{4!}\right)}^3\int dz \int dw \int dv \phi_z\phi_z\phi_z\phi_z \phi_w\phi_w\phi_w\phi_w \phi_v\phi_v\phi_v\phi_v \right> $$

There are four (4) ways to connect x to z and then three (3) ways to connect y to z. There are four ways (4) to connect one of the remaining zs to a w and four ways to connect the other remaining z to a v (4), this can be done for either of the two remaining zs (2), i.e., the "third" z can connect to w or the "fourth" z can connect to w. There are six (3!) ways to connect up the remaining ws and vs. And finally, there is nothing special about "z", I can treat "w" the same way as "z" or "v" the same way as "z", so that gives another factor of three (3).

So the overall symmetry factor is: $$ 4*3*4*4*2*3*2*3\frac{1}{3!}\frac{1}{4!^3}=\frac{1}{12} $$

Answer 2

Contrary to your previous question Problem understanding the symmetry factor in a feynman diagram the roles of the three vertices are not different so you have from the expansion of the exponential a $1/3!$ but it does not get compensated by the choice of role assignement. Here this choice amounts to deciding who connects directly to $x$ and $y$ and that's it. So you have $\frac{3}{3!}=\frac{1}{2}$. Also the symmetry group has order 12 because you can permute the 3 lines of the embedded sunshine diagram and you can also rotate it with repect to a vertical axis.