Computing symmetry/combinatorial factor for a diagram in $\phi^4$ theory

Question

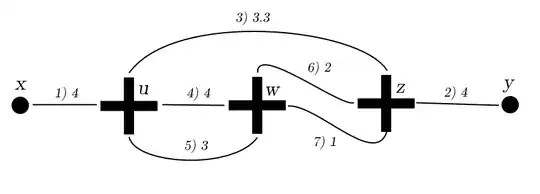
I am working with $\lambda\phi^4/4!$ theory and am struggling to compute the symmetry factor for the diagram 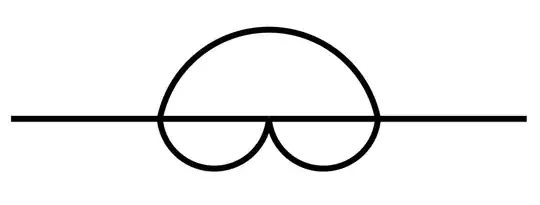by using the method specified here. I know that the answer is ${1}/{12}$, but I can't work out how to get this.

Here is my reasoning:

0. the vertices are indistinguishable, so there is a factor of $3!$
1. 4 ways of choosing which leg of $u$ to connect to $x$
2. 4 ways of choosing which leg of $z$ to connect to $y$
3. 3 ways of choosing a leg of $u$ to connect to $z$, and 3 ways of choosing which leg of $z$ it should be connected to
4. 4 choices for connecting the first leg of $u$ to a leg of $w$
5. 3 choices for connecting the second leg of $u$ to the remaining legs of $w$
6. 2 ways to connect one of the last two legs of $w$ to $z$
7. 1 way to connect the final leg of $w$ to the final leg of $z$

The overall factor is then (with a factor of ${1}/{4!^3 3!}$ from the Dyson expansion) $$ \frac{1}{S} = \frac{1}{3!\cdot (4!)^3} \cdot 3! \cdot 4\cdot 4 \cdot 3 \cdot 3 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = \frac{4^2 \cdot 3^2}{4!^2} = \frac{1}{4}. $$

I would be very grateful if anyone could point out where I have gone wrong. Alternatively, if anyone could explain another systematic way to compute symmetry factors for general Feynman diagrams then that would also be very helpful!