Symmetry factor in Srednicki?

Question

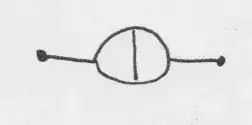
The following diagram is given in Srednicki pg62 figure 9.7:

Srednicki gives this diagram a symmetry factor of $S=2^2=4$. But using a method which seems to work on every other diagram I get $S=2$ (the method is given below). Am I missing a subtly here or is the symmetry factor given in the book wrong?

My Method

We split each of the vertices into 3 and count the number of ways we can draw each line between two vertices (as shown below): The number in front of the brackets gives the number of ways whilst the number in brackets gives the order which I chose them. On top of this we have a factor of $^4C_2 \times 2$ for swapping the $4$ vertices (taking into account that two vertices are identical). This thus gives us a symmetry factor of: $$S^{-1}=\frac{3\times 3\times 6 \times 6\times 2 \times 2 \times 1}{(3!)^4 \times 4!} \times{^4C_2}\times 2$$ $$=\frac{3\times 3\times 6 \times 6\times 2 \times 2 \times 1}{(3!)^4 \times 4!} \frac{4!}{2!2!}\times 2$$ $$=1/2$$ Thus $S=2$

Answer 1

You are right. You are basically using method 1) from my answer to Problem understanding the symmetry factor in a feynman diagram and you handled it like a champ. If you use method 2) from that same answer you will also find there is only one nontrivial automorphism. Think of the graph as a "theta" taking a nap on a hammock attached to the axis given by the two external legs. This autmorphism is the rotation by 180 degrees around this axis.

PS: If you have seen two-stage experiments in elementary probability or more general counting methods based on decision trees, then this is basically what you are doing. I recommend to first choose the vertices: 4 choices for the neighbor of the left external leg times 3 choices for the right leg neighbor, and then looking at the internal line contraction count. Of course $4\times 3={}^{4}C_{2}\times 2$.

---

Edit as per AFT's comment: The above answer is based on the assumption that one is computing a two-point function rather than a vacuum diagram. Note that the issue of symmetry factors is a question that belongs to mathematics rather physics. The proper setting for handling these factors with rigor and accuracy is Joyal's theory of combinatorial species: https://en.wikipedia.org/wiki/Combinatorial_species . You can see how one can apply it to the specific context of Feynman diagrams in my article "Feynman Diagrams in Algebraic Combinatorics". The article focuses on a complex bosonic model with $\bar{\phi}\phi^n$ interaction but it is straightforward to transpose it to that of a real scalar $\phi^3$ model as in the OP's question.

Answer 2

TL;DR: Srednicki is in the source-picture/$J$-picture where each external leg of a Feynman diagram is connected to a $J$-source, which is denoted by a fat black bullet. The caption of Fig. 9.7 says that there are $E=2$ external legs and $V=4$ vertices. Since the two $J$-sources are identical, that yields another $\mathbb{Z}_2$-automorphism, bringing the total symmetry factor to $S=4$.

References:

1. M. Srednicki, QFT, 2007; Fig. 9.7. A prepublication draft PDF file is available here.