Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 37
Beside the three vertices of a triangle, there are further characteristic points of a triangle, as its centroid (center of gravity), the circumcenter, the incenter and the orthocenter.
- Medians and centroid
For a set of points in an affine space over a real vector space , the barycentric combination
is called the center of gravity
of these points.This is also called the centroid of the points. It just the barycentric combination of the points where every point enters with the same weight. For two points , the center of gravity is also called the midpoint of the two points (or of the line segment ). In the case of two real numbers, we also talk about the arithmetic mean of the numbers. For , the centroid of the points is also the centroid of its convex hull. The centroid of the three points is also the intersection point of the medians of the triangle.
The median through runs through the point and the midpoint of the opposite side of the triangle.
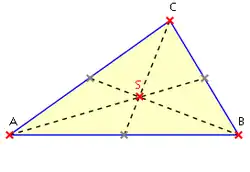
In a nondegenerate triangle in the Euclidean plane, the three medians
intersect in the centroid of the triangle.We have
and this is a point of the median through . Due to the symmetry of the situation, this point also lies on the other medians.
In particular, the centroid divides every median with the ratio , the longer part being closer to the vertex.
- Perpendicular bisectors and circumcenter
For two points in the Euclidean plane, the line that is perpendicular to the line given by and , and that runs through the midpoint of the line segment between and , is called the perpendicular bisector
of the line segment.The perpendicular bisector can be described as
where is an arbitrary vector perpendicular to . If and are given in Cartesian coordinates, then the perpendicular bisector is
Let be different points in a Euclidean plane. Then the perpendicular bisector of and consists of all those points that have the same distance to
and to .Proof
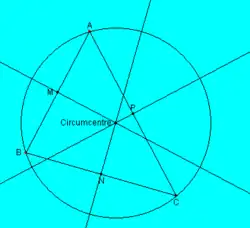
The perpendicular bisectors of the three sides in a nondegenerate triangle in the
Euclidean plane intersect in one point. All vertices of the triangle have the same distance to this intersecting point.The perpendicular bisector for the line segment between and consists, according to Lemma 37.5 , exactly of those points of the plane that have to these points the same distance. Therefore, the intersecting point of the perpendicular bisector of and and the perpendicular bisector of and has the same distance to all three vertices. This gives the supplement, and also, that all three perpendicular bisectors meet in this point.
The intersecting point of the three perpendicular bisectors in a nondegenerate triangle in the Euclidean plane is called the
circumcenter.The circumcenter is the center of the circumcircle; this is the circle that contains all three vertices of the triangle.
- Angle bisectors and incenter
For two linearly independent vectors and in a normed real vector space , the line generated by
is called the angle bisector
of the two vectors.We define here the angle bisectors without referring to an angle, we do not even suppose that an inner product is given. However, if both vectors are in a Euclidean space, then an easy consideration (see Exercise 37.13 ) show that the angle bisector cut indeed the angle into halves. The definition works also for an affine space over a normed vector space; three non-collinear points define an angle bisector for every point involved.
Let be linearly independent vectors in . Then every point of the angle bisector of and has the same distance to the lines and to . If a point has the same distance to and to , then it belongs to the angle bisector of and or to the angle bisector of
and .We may assume that and are normed. Let . Due to Corollary 35.7 , we have
and, accordingly,
Therefore, the distances coincide if and only if
holds. If
then
and the equation holds. For the reverse statement, we may write
From
we can deduce
therefore,
Because and are normed and linearly independent, Exercise 31.9 implies that
hence, the right-hand factor is not , and, therefore, . In case
a similar consideration gives .
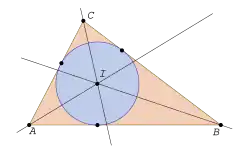
The three angle bisectors in a nondegenerate triangle meet in one intersecting point, which has the same distance to every side of the triangle. If the vertices are given by , and if the side lengths are denoted by , then this intersecting point has the coordinates
Due to Lemma 37.9 , the angle bisector for consists of points that have the same distance to the line of the adjacent sides and . Accordingly, the angle bisector for consists of points that have the same distance to the lines and . Therefore, the intersecting point of these two angle bisectors has the same distance to all three sides.
In order to determine the coordinates, we write the angle bisector of as
that is,
Equating with the angle bisector of , we obtain
The solution is given by
and
because this gives, after inserting, the symmetric expression
This is also the intersecting point of all three angle bisectors.
The intersecting point of the three angle bisectors in a nondegenerate triangle in the Euclidean plane is called
incenter.The circle around the incenter that meets all three sides of the triangles tangentially, is called incircle.
- The orthocenter
Let be the circumcenter, and let be the centroid of a nondegenerate triangle in the Euclidean plane. Then the point
lies on every altitude
of the triangle. In particular, the three altitudes intersect in one point.We move to the origin, so that the points have the same norm. The point in question is just . The vector of the line given by this point and is . This line runs through , and we have
Due to the equality of the norms, this is ; therefore, this line is the altitude line through .
For a nondegenerate triangle in a Euclidean plane, the intersecting point of the three altitudes is called the
orthocenter.
- The Euler line
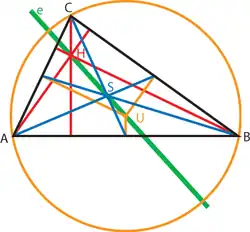
The centroid, the circumcenter, and the orthocenter of a nondegenerate triangle in the
Euclidean plane lie on a line.This follows directly from Lemma 37.12 .
If the triangle is equilateral, then the three points coincide and there are many lines running through this point. If the triangle is not equilateral, then these points are not equal
(see
Exercise 37.2
)
and there is exactly one line given by these three points. It is called the Euler line.
- The nine-point circle
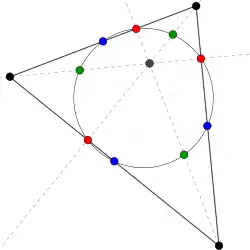
Let a nondegenerate triangle in the Euclidean plane with vertices be given. Let be the circumcircle of the midpoints
of the sides of the triangle. Then the following statements hold.- The radius of is half of the radius of the circumcircle of .
- The line segements between the orthocenter and the vertices are cut in halves by .
- The feet of the altitudes of lie on .
- Let be the
circumcenter
of the triangle; we may assume that this point is the origin of a Cartesian coordinate system. We consider the point
The distance between the midpoint of the side connecting and and is
Since the norms of all vertices are equal due to the choice of , it follows that is the circumcenter of the triangle given by the midpoints of the original triangle, and that its radius is the half of the radius of the circumcircle.
- By
Lemma 37.12
,
is the
orthocenter.
Therefore, the midpoint of the line segment between and the orthocenter equals
The distance between this point and is
- Note that the points constructed in (1) and (2) lie on the circle opposite to each other. Indeed, we have
which is the center of . Hence, for each side, its midpoint, the midpoint between the opposite vertex and the orthocenter, and the foot of the corresponding altitude form a right triangle. Its circle with the hypotenuse as diameter equals .
The circle in the preceding statement is called the Nine-point circle, or the Feuerbach circle.
| << | Linear algebra (Osnabrück 2024-2025)/Part II | >> PDF-version of this lecture Exercise sheet for this lecture (PDF) |
|---|