Linear algebra (Osnabrück 2024-2025)/Part II/Lecture 36

Triangles

In this and the next lecture, we are dealing with triangles. A triangle is just a tuple ${}(A,B,C)$ of three points (called vertices) in an affine space ${}E$ (typically, an affine plane) over a Euclidean space ${}V$ . We allow the situation that some or all vertices coincide (a degenerate triangle), and we identify triangles if they only differ by the ordering of the vertices. A triangle is by definition not degenerate if and only if the three points are affinely independent. Quite often, we regard a triangle as its convex hull, that is, the set

{\left\{rA+sB+tC\mid r+s+t=1,\,0\leq r,s,t\leq 1\right\}}

of all barycentric combinations of the three points, where all coefficients are not negative. The connecting segment

{}{\overline {A,B}}={\left\{rA+sB\mid r+s=1,\,0\leq r,s\leq 1\right\}}\,

is called the edge between the vertices ${}A$ and ${}B$ (or the edge opposite of ${}C$ ). It is often denoted by ${}c$ , its length is

{}d(A,B)=\Vert {\overrightarrow {AB}}\Vert \,.

The corresponding denominations hold for the other edges. Sometimes we also denote the lengths of the edges by ${}a,b,c$ . The angle ${}\angle (A,B,C)$ of the triangle at the vertex ${}B$ is defined as

\angle ({\overrightarrow {BA}},{\overrightarrow {BC}}),

accordingly for the other vertices. The angles are usually denoted by ${}\alpha ,\beta ,\gamma$ .

Definition

Two triangles in a Euclidean plane are called congruent if they can be transformed into each other by the composition of a translation and an

isometry.

We also say that congruent triangles can be transformed into each other by an affine-linear isometry.

Theorem

Two triangles in a Euclidean plane are congruent

to each other if and only if their edge lengths coincide.

Proof

Translations and isometries preserve lengths; therefore, congruent triangles have the same lengths of edges. Let now two triangles ${}(A,B,C)$ and ${}(A',B',C')$ be given, having the same edge lengths. After renaming, we may assume that the edge lengths fulfill the relation

{}d(A,B)\geq d(A,C)\geq d(B,C)\,,

and that the same holds for the second triangle. We can assume ${}E=\mathbb {R} ^{2}$ , and we can also assume after a translation that ${}A=A'=0$ holds. After rotations of the triangles around the origin, we may further assume that ${}B$ as well as ${}B'$ lie on the positive ${}x$ -axis. Because of the length equality, we have ${}B=B'$ . The points ${}C$ and ${}C'$ have, on one hand, the same distance to ${}0$ , and, on the other hand, the same distance to ${}B$ . That is, they lie on the intersection of a circle about ${}0$ and a circle about ${}B$ . Since there are only two intersection points, we have either ${}C=C'$ , or ${}C$ and ${}C'$ can be transformed to each other by a reflection at the ${}x$ -axis.

\Box

Definition

Two triangles in a Euclidean plane are called properly congruent if they can be transformed into each other by the composition of a translation and a

proper isometry.

Definition

Two triangles in a Euclidean plane are called similar if they can be transformed into each other by the composition of a translation and an

angle-preserving mapping.

Theorem

Two triangles in a Euclidean plane are similar

to each other if and only if their angles coincide.

Proof

See Exercise 36.12 .

\Box

The Pythagorean theorem

We first deal with right triangles.

Definition

A triangle ${}(A,B,C)$ is called a right triangle if for one vertex the adjacent edges are perpendicular

to each other.

Definition

In a right triangle, the side opposite to the right angle is called the hypotenuse

of the right triangle.

Definition

In a right triangle, the sides adjacent to the right angle are called the catheti (or legs)

of the right triangle.

The Pythagorean theorem for a right triangle says the following.

Theorem

In a right triangle, the area of the square of the hypotenuse

equals the sum of the areas of the squares of the two other sides.

Proof

We denote the vertices of the triangle by ${}A,B,C$ , with the right angle located at ${}C$ . We set ${}v=C-A$ , and ${}w=B-C$ . The vector from ${}A$ to ${}B$ equals ${}v+w$ , and ${}v$ and ${}w$ are perpendicular to each other. Therefore,

{}\Vert {v+w}\Vert ^{2}=\left\langle v+w,v+w\right\rangle =\left\langle v,v\right\rangle +2\left\langle v,w\right\rangle +\left\langle w,w\right\rangle =\Vert {v}\Vert ^{2}+\Vert {w}\Vert ^{2}\,.

\Box

In this formulation, we use that the area of a square (that is, of the geometric object) equals the (arithmetic) square of the side lengths. The proof does not refer to areas.

Definition

For a triangle ${}A,B,C$ in a Euclidean plane, the line running through ${}A$ and being perpendicular to the line given by ${}B$ and ${}C$ , is called the altitude line through ${}A$ . The line segment from ${}A$ to the line given by ${}B$ and ${}C$ is called the altitude

through

{}A

.

The length of the altitude is also called the altitude.

Definition

In a triangle ${}A,B,C$ in a Euclidean plane, the intersecting point of the altitude line through ${}A$ with the line given by ${}B$ and ${}C$ is called the foot

of this altitude.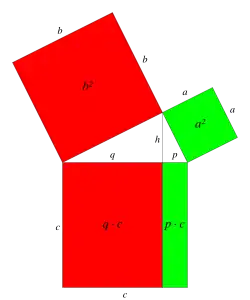

Der following theorem is called the Cathetus theorem.

Theorem

Let ${}A,B,C$ be a right triangle, with the right angle located at ${}C$ . Let ${}h$ denote the altitude through ${}C$ , and let ${}D$ denote the foot of this altitude on the line given by ${}A$ and ${}B$ . Then

{}d(A,C)^{2}=d(A,D)\cdot d(A,B)\,.

Proof

We set ${}v=C-A$ , and ${}w=B-C$ . The vector from ${}A$ to ${}B$ equals ${}v+w$ . Due to Lemma 32.14 , the foot of the altitude is

{}{\begin{aligned}D&=A+p_{(v+w)\mathbb {R} }(v)\\&=A+\left\langle v,{\frac {v+w}{\Vert {v+w}\Vert }}\right\rangle {\frac {v+w}{\Vert {v+w}\Vert }}\\&=A+{\frac {\left\langle v,v\right\rangle }{\Vert {v+w}\Vert ^{2}}}(v+w)\\&=A+{\frac {\left\langle v,v\right\rangle }{\left\langle v,v\right\rangle +\left\langle w,w\right\rangle }}(v+w).\end{aligned}}

Hence, we obtain

{}{\begin{aligned}d(A,D)\cdot d(A,B)&={\frac {\left\langle v,v\right\rangle }{\left\langle v,v\right\rangle +\left\langle w,w\right\rangle }}\Vert {v+w}\Vert \cdot \Vert {v+w}\Vert \\&={\frac {\left\langle v,v\right\rangle }{\left\langle v,v\right\rangle +\left\langle w,w\right\rangle }}\left\langle v+w,v+w\right\rangle \\&=\left\langle v,v\right\rangle \\&=\Vert {v}\Vert ^{2}\\&=d(A,C)^{2}.\end{aligned}}

\Box

The following theorem is called the Right triangle altitude theorem.

Theorem

Let ${}A,B,C$ be a right triangle, with the right angle located at ${}C$ . Let ${}h$ be the altitude through ${}C$ , and let ${}D$ denote the foot of this altitude through the linen given by ${}A$ and ${}B$ . Then

{}d(C,D)^{2}=d(A,D)\cdot d(B,D)\,.

Proof

See Exercise 36.20 .

\Box

The following theorem is called the Law of cosines.

Theorem

Let a triangle ${}(A,B,C)$ be given, with side lengths ${}a,b,c$ . Let ${}\gamma$ denote the angle at ${}C$ . Then

{}c^{2}=a^{2}+b^{2}-2ab\cos \gamma \,

holds.

Proof

See Exercise 36.22 .

\Box

Thales's theorem

Theorem

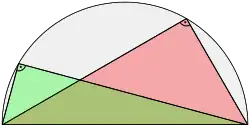
Let ${}P$ be a point in the Euclidean plane ${}E$ , let ${}K$ be a circle with center ${}P$ , and let ${}G$ be a line through ${}P$ , intersecting the circle in the points ${}A$ and ${}B$ . Then for every point ${}C\in K$ ,

the triangle

{}A,B,C

is a right triangle with the right angle at

{}C

.

Proof

Without loss of generality, we may assume that ${}E=\mathbb {R} ^{2}$ and ${}P=0$ ; we denote the radius by ${}r$ . We write ${}w=C$ , ${}v=A$ , ${}B=-v$ . The vector from ${}A$ to ${}C$ is ${}-v+w$ , and the vector from ${}B$ to ${}C$ is ${}v+w$ . Therefore,

{}{\begin{aligned}\left\langle -v+w,v+w\right\rangle &=\left\langle -v,v\right\rangle +\left\langle -v,w\right\rangle +\left\langle w,v\right\rangle +\left\langle w,w\right\rangle \\&=-\left\langle v,v\right\rangle -\left\langle v,w\right\rangle +\left\langle v,w\right\rangle +\left\langle w,w\right\rangle \\&=-\left\langle v,v\right\rangle +\left\langle w,w\right\rangle \\&=-r^{2}+r^{2}\\&=0.\end{aligned}}

This means that the two sides of the triangle meeting at ${}C$ are perpendicular to each other.

\Box

The intercept theorems

We formulate in the language of linear algebra the intercept theorems. We work in the setting of a two-dimensional Euclidean vector space, which provides lengths of line segments. Two affine lines are called parallel if they are spanned by the same vector. We formulate the intercept theorems in such a way that the intersecting point of the rays lies in the origin. This can always be achieved by translating the intersecting point to the origin, as this does not change the lengths.

Theorem

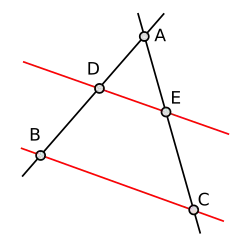
Let ${}V$ denote a two-dimensional Euclidean vector space, let ${}s_{1},s_{2},v\in V$ be vectors, and suppose that ${}v$ and ${}s_{1}$ are linearly independent, and that ${}v$ and ${}s_{2}$ are linearly independent. Let ${}S_{1}=\mathbb {R} s_{1}$ and ${}S_{2}=\mathbb {R} s_{2}$ denote the lines (the rays) defined by ${}s_{1}$ and ${}s_{2}$ . Let ${}P$ and ${}Q$ be points in ${}V$ with the corresponding parallel lines ${}G=P+\mathbb {R} v$ and ${}H=Q+\mathbb {R} v$ . We denote the intersecting points (which exist uniquely due to the condition) by

A_{1}=S_{1}\cap G,\,A_{2}=S_{2}\cap G,\,B_{1}=S_{1}\cap H,\,B_{2}=S_{2}\cap H,

and suppose that ${}A_{1},B_{1}\neq 0$ . Then

{}{\frac {d(B_{1},B_{2})}{\Vert {B_{1}}\Vert }}={\frac {d(A_{1},A_{2})}{\Vert {A_{1}}\Vert }}\,.

Proof

Without loss of generality, we may assume that ${}s_{1}=A_{1}$ , ${}s_{2}=A_{2}$ , and ${}v=A_{2}-A_{1}$ , as this does not change the lines involved. We write ${}B_{1}=tA_{1}$ . We have ${}A_{2}=A_{1}+v$ ; therefore, we obtain

{}tA_{2}=tA_{1}+tv=B_{1}+tv\,.

This point belongs to ${}S_{2}$ and also to ${}H$ . This means that this point is just ${}B_{2}$ . Hence, ${}B_{2}=tA_{2}$ , and

{}{\frac {\Vert {B_{1}-B_{2}}\Vert }{\Vert {B_{1}}\Vert }}={\frac {\Vert {tA_{1}-tA_{2}}\Vert }{\Vert {tA_{1}}\Vert }}={\frac {\Vert {A_{1}-A_{2}}\Vert }{\Vert {A_{1}}\Vert }}\,.

\Box

In particular, the preceding theorem says that in the given situation, the ratios of corresponding side lengths of the triangles ${}0,A_{1},A_{2}$ and ${}0,B_{1},B_{2}$ are the same. These triangles are similar; the triangle ${}0,B_{1},B_{2}$ arises from the triangle ${}0,A_{1},A_{2}$ by a homothety with factor ${}t$ . This factor describes all length relations.

An application of the intercept theorem. One can compute the width of the river without crossing the river.

Another application of the intercept theorem is to guess a distance using one thumb but two eyes.

Corollary

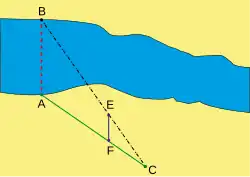
Let ${}V$ denote a two-dimensional Euclidean vector space, let ${}s_{1},s_{2},v\in V$ be vectors, and suppose that ${}v$ and ${}s_{1}$ are linearly independent, and that ${}v$ and ${}s_{2}$ are linearly independent. Let ${}S_{1}=\mathbb {R} s_{1}$ and ${}S_{2}=\mathbb {R} s_{2}$ denote the lines defined by ${}s_{1}$ and ${}s_{2}$ . Let ${}P$ and ${}Q$ be points in ${}V$ with the corresponding parallel lines ${}G=P+\mathbb {R} v$ and ${}H=Q+\mathbb {R} v$ . We denote the intersecting points (which exist uniquely due to the condition) by

A_{1}=S_{1}\cap G,\,A_{2}=S_{2}\cap G,\,B_{1}=S_{1}\cap H,\,B_{2}=S_{2}\cap H,

and suppose that ${}A_{1},A_{2},A_{1}-A_{2}\neq 0$ . Then

{}{\frac {d(B_{1},B_{2})}{d(A_{1},A_{2})}}={\frac {\Vert {B_{1}}\Vert }{\Vert {A_{1}}\Vert }}={\frac {\Vert {B_{2}}\Vert }{\Vert {A_{2}}\Vert }}\,.

Proof

This follows directly from Theorem 36.16 .

\Box

In particular, we have the equation

{}{\frac {\Vert {B_{1}}\Vert }{\Vert {A_{1}}\Vert }}={\frac {\Vert {B_{2}}\Vert }{\Vert {A_{2}}\Vert }}\,,

which only takes the lengths on the rays into account.

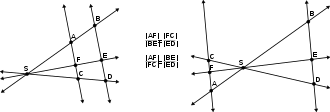
In the last variant of the intercept theorem, there are three rays.

Theorem

Let ${}V$ be a two-dimensional Euclidean vector space, let ${}s_{1},s_{2},s_{3}\in V$ be vectors, and suppose that ${}v\in V$ is linearly independent to each of these vectors. Let ${}S_{i}=\mathbb {R} s_{i}$ , ${}i=1,2,3$ , be the lines defined by the ${}s_{i}$ . Let ${}P$ and ${}Q$ be points in ${}V$ with den corresponding parallel lines ${}G=P+\mathbb {R} v$ and ${}H=Q+\mathbb {R} v$ . We denote the intersecting points of the lines (which exist uniquely due to the conditions) by