Triangle geometry/Perpendicular bisector/Introduction/Section

Definition

For two points ${}A\neq B$ in the Euclidean plane, the line that is perpendicular to the line given by ${}A$ and ${}B$ , and that runs through the midpoint of the line segment between ${}A$ and ${}B$ , is called the perpendicular bisector

of the line segment.

The perpendicular bisector can be described as

{\frac {A+B}{2}}+s(B-A)^{\perp },\,s\in \mathbb {R} ,

where ${}(B-A)^{\perp }$ is an arbitrary vector ${}\neq 0$ perpendicular to ${}B-A$ . If ${}A={\begin{pmatrix}a_{1}\\a_{2}\end{pmatrix}}$ and ${}B={\begin{pmatrix}b_{1}\\b_{2}\end{pmatrix}}$ are given in Cartesian coordinates, then the perpendicular bisector is

{\frac {1}{2}}{\begin{pmatrix}a_{1}+b_{1}\\a_{2}+b_{2}\end{pmatrix}}+s{\begin{pmatrix}b_{2}-a_{2}\\-b_{1}+a_{1}\end{pmatrix}},\,s\in \mathbb {R} .

Lemma

Let ${}A,B$ be different points in a Euclidean plane. Then the perpendicular bisector of ${}A$ and ${}B$ consists of all those points that have the same distance to

{}A

and to

{}B

.

Proof

See exercise.

\Box

Theorem

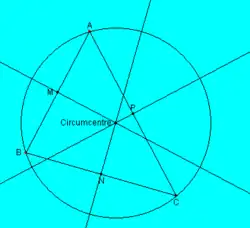
The perpendicular bisectors of the three sides in a nondegenerate triangle in the

Euclidean plane intersect in one point. All vertices of the triangle have the same distance to this intersecting point.

Proof

The perpendicular bisector for the line segment between ${}A$ and ${}B$ consists, according to fact, exactly of those points of the plane that have to these points the same distance. Therefore, the intersecting point ${}P$ of the perpendicular bisector of ${}A$ and ${}B$ and the perpendicular bisector of ${}A$ and ${}C$ has the same distance to all three vertices. This gives the supplement, and also, that all three perpendicular bisectors meet in this point.

\Box

Definition

The intersecting point of the three perpendicular bisectors in a nondegenerate triangle in the Euclidean plane is called the

circumcenter.

The circumcenter is the center of the circumcircle; this is the circle that contains all three vertices of the triangle.