Why doesn't the Moon fall onto the Earth?

Question

Why doesn't the Moon fall onto the Earth? For that matter, why doesn't anything rotating a larger body ever fall onto the larger body?

Answer 1

The moon does not fall to Earth because it is in an orbit.

One of the most difficult things to learn about physics is the concept of force. Just because there is a force on something does not mean it will be moving in the direction of the force. Instead, the force influences the motion to be a bit more in the direction of the force than it was before.

For example, if you roll a bowling ball straight down a lane, then run up beside it and kick it towards the gutter, you apply a force towards the gutter, but the ball doesn't go straight into the gutter. Instead it keeps going down the lane, but picks up a little bit of diagonal motion as well.

Imagine you're standing at the edge of a cliff 100m tall. If you drop a rock off, it will fall straight down because it had no velocity to begin with, so the only velocity it picks up is downward from the downward force.

If you throw the rock out horizontally, it will still fall, but it will keep moving out horizontally as it does so, and falls at an angle. (The angle isn't constant - the shape is a curve called a parabola, but that's relatively unimportant here.) The the force is straight down, but that force doesn't stop the rock from moving horizontally.

If you throw the rock harder, it goes further, and falls at a shallower angle. The force on it from gravity is the same, but the original velocity was much bigger and so the deflection is less.

Now imagine throwing the rock so hard it travels one kilometer horizontally before it hits the ground. If you do that, something slightly new happens. The rock still falls, but it has to fall more than just 100m before it hits the ground. The reason is that the Earth is curved, and so as the rock traveled out that kilometer, the Earth was actually curving away underneath of it. In one kilometer, it turns out the Earth curves away by about 10 centimeters - a small difference, but a real one.

As you throw the rock even harder than that, the curving away of the Earth underneath becomes more significant. If you could throw the rock 10 kilometers, the Earth would now curve away by 10 meters, and for a 100 km throw the Earth curves away by an entire kilometer. Now the stone has to fall a very long way down compared to the 100m cliff it was dropped from.

Check out the following drawing. It was made by Isaac Newton, the first person to understand orbits. IMHO it is one of the greatest diagrams ever made.

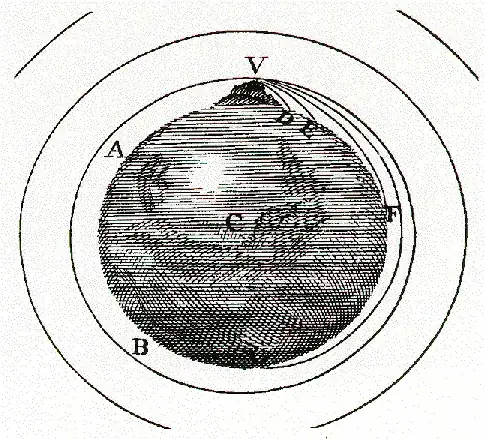
What it shows is that if you could throw the rock hard enough, the Earth would curve away from underneath the rock so much that the rock actually never gets any closer to the ground. It goes all the way around in the circle and might hit you in the back of the head!

This is an orbit. It's what satellites and the moon are doing. We can't actually do it here close to the surface of the Earth due to wind resistance, but on the surface of the moon, where there's no atmosphere, you could indeed have a very low orbit.

This is the mechanism by which things "stay up" in space.

Gravity gets weaker as you go further out. The Earth's gravity is much weaker at the moon than at a low-earth orbit satellite. Because gravity is so much weaker at the moon, the moon orbits much more slowly than the International Space Station, for example. The moon takes one month to go around. The ISS takes a few hours. An interesting consequence is that if you go out just the right amount in between, about six Earth radii, you reach a point where gravity is weakened enough that an orbit around the Earth takes 24 hours. There, you could have a "geosynchronous orbit", a satellite that orbits so that it stays above the same spot on Earth's equator as Earth spins.

Although gravity gets weaker as you go further out, there is no cut-off distance. In theory, gravity extends forever. However, if you went towards the sun, eventually the sun's gravity would be stronger than the Earth's, and then you wouldn't fall back to Earth any more, even lacking the speed to orbit. That would happen if you went about .1% of the distance to the sun, or about 250,000 km, or 40 Earth radii. (This is actually less than the distance to the moon, but the moon doesn't fall into the Sun because it's orbiting the sun, just like the Earth itself is.)

So the moon "falls" toward Earth due to gravity, but doesn't get any closer to Earth because its motion is an orbit, and the dynamics of the orbit are determined by the strength of gravity at that distance and by Newton's laws of motion.

note: adapted from an answer I wrote to a similar question on quora

Answer 2

The moon is continuously falling towards the earth but missing all the time! Same with other planets too.

In general, in an inverse square central force field one can calculate the trajectory of a particle and verify that the trajectory is either a parabola or ellipse or hyperbola (conic sections) depending upon the initial position and initial momentum of the particle. For a two body system with certain initial conditions, it is a stable elliptical orbit. In case of the sun and the earth it is an ellipse (ignoring gravitation of other objects and also ignoring the relativistic precession of orbit).

This page has a nice video.

Answer 3

The truth is that the moon IS constantly trying to fall upon the earth, due to the force of gravity; but it is constantly missing, due to its tangential velocity.

To understand this, think of whirling a rock, tied to the end of a string, around and around, with your hand just above your head. As the rock travels in circles it is constantly being pulled toward you by the force on the string (which is like Earth's pull of gravity on the moon). Why doesn't the rock come bonk you on the head, if you are constantly pulling it toward your head? The answer is that the rock is always trying to change its velocity vector to come do just that; but the change is only enough to just keep it in a circular path, like the pull on the Moon is just enough to keep it in a circular orbit around Earth.

Answer 4

Another way to look at it: In the frame of reference of earth, the moon has angular momentum. Angular momentum is preserved if no torque is applied ($\tau=dL/dt$).

The gravity forces between earth and the moon are in the direction of the center of mass, so they produce no torque ($\tau=mv\times R$), so the angular momentum ($L$) cannot change.

Gravity is perpendicular to the moon's speed, so it changes the direction and not the magnitude of the speed itself. $L=mv\times R$ and if $L$, $m$ and $v$ are constant, $R$ must remain constant as well, so the radius doesn't change.

Answer 5

The best simple answer I can think of are this: An orbit of one body of an another is essentially a degree of balance among forces, real and fictitious. These would include centripetal force (gravity) attracting the orbiting body ("the fall") and centrifugal force which arises out of the orbiting body's inertia (the orbiting body's tendency to remain in a constant linear motion away from the body it is orbiting). In General Relativistic terms, the orbit is the result of a body moving in a straight line through the curved space that exists around the more massive body. If the lesser body moves with the sufficient combination of momentum and distance it will continue to pass the more massive body onto other regions of space. If that combination is not sufficient to overcome the curvature of space in the region around the more massive body then the lesser body will continue it's tendency to travel in a straight line but it must it do so in a curved space that it cannot "escape". If it has a sufficient minimum momentum, it's tendency to move in a straight line away from the more massive body will overcome the downward curvature. These two conditions will cause the lesser body, per Newton, to become the perpetual satellite of the more massive body because the lesser body must stay in motion unless an equal and opposite force is applied to it's motion. The lesser body doesn't experience resistance from friction or air in space and the gravitational force is perpendicular, not opposite to the motion of the lesser body so absent an equal and opposite force, the lesser body continues its trek about the more massive body indefinitely while it's momentum is in balance with the massive body's gravity.

Answer 6

The original question is:

Why doesn't the Moon, or for that matter anything rotating another larger body, ever fall into the larger body?

Others have answered that the centrifugal forces equal the centripetal forces, so the moon stays in an orbit of the earth.

Satellites orbit the earth for the same reason. However, satellite orbits sometimes decay, so the satellite "orbit" changes to a collapsing spiral, and eventually the satellites do come back down to earth (normally burning up from atmospheric friction). Orbits can end in the other direction too, where the satellite moves away from earth in an enlarging spiral, eventually escaping earth's gravity entirely.

Answer 7

as we know that the moon is revolving around the earth in circular path where centripetal force is developed by the gravitation and then outward force the outcome of the circular motion "centrifugal force is balancing the centripetal force.

Answer 8

The Moon does not fall towards Earth right now because Earth rotates itself. The energy from the Earth's own rotation around its axis is gradually tranferred into energy of the Moon's orbital motion. That's why the Earth's rotating speed decreases but the distance to the Moon increases.

This process will continue until Earth's proper rotation will slow to the point where it has the same angular velocity as the Moon's orbital motion. From that moment on the Moon will start to gradually approach Earth.

Answer 9

One point which these answers miss concerns frame dragging.

The planet Earth is a massive body, therefore it generates (or causes) gravity; but it is also a rotating body. The Moon, being close enough to the Earth to be captured by the Earth's gravity, so that it is in orbit, is nonetheless not so close that its orbital motion is retarded by contact with atmospheric molecules (which cause a drag - a deceleration - on objects in low Earth orbit).

Because the Moon is in a prograde orbit (i.e. it is orbiting in the same direction as the Earth is rotating), the Earth's (rotating) gravity is continuously accelerating the Moon (because the Earth rotates 28 times in the time the Moon takes to rotate once: i.e. 28 days); so that, over time, the Moon's momentum is increasing -- such that it is getting further away from the Earth: a phenomenon historically termed frame dragging or rotation dragging.

This type of acceleration was identified by Einstein in his General Theory of Relativity, and is fairly well understood. The Moon becomes a few inches further from the Earth over the course of a hundred years, so gradually is moving towards escaping from its orbit, but theory predicts that because the effect is so slow the solar system will cease to exist before sufficient time can pass for the effect to cause the Moon to actually escape from Earth orbit.

This acceleration applies to any natural or artificial body in a (prograde) orbit about a planetary mass which is rotating (and if the orbit is retrograde the same effect will decelerate it).

So the real answer to the original question is that it is impossible for a satellite in a stable orbit about a body of planetary mass to fall out of the sky, unless (a) the planet is not rotating, or (b) the planetary atmosphere causes drag effects on the satellite, or (c) the satellite is in a retrograde orbit. Where none of these things occur, it is impossible for the distance between the satellite and the planet to decrease, because the satellite's momentum cannot decrease, so its outward motion (i.e. its angular momentum) cannot lessen.