A show on the weather channel said that as a water molecule ascends in the atmosphere it cools. Does it make sense to talk about the temperature of a single molecule?
10 Answers
Without intending any disrespect, I'm quite surprised that several very knowledgeable people have given a wrong, or at least incomplete, answer to this old question.
For a single molecule that is in complete isolation, it is indeed generally not true (or at least not useful) to assign it a temperature, as others have said. Such a system would be more naturally described in the so-called microcanonical ensemble of thermodynamics, and since it can have a well-defined and conserved energy, the usual role of temperature in determining the probability of occupation of different energy states via a Boltzmann distribution is not relevant. Put simply, temperature is only relevant when there is uncertainty about how much energy a system has, which need not be true when it is isolated*.
However, things are different when you have a molecule in an open system, which can freely exchange energy with its surroundings, as is certainly the case for the specific example the OP has described. In this case, as long as the molecule is in equilibrium or quasi-equilibrium with its surroundings, it does indeed have a well-defined temperature. If there are no other relevant conserved quantities, the quantum state of the molecule is described by a diagonal density matrix in the single-particle energy basis that follows the Boltzmann distribution, $\rho=Z^{-1} e^{-\beta H}$ . Practically speaking, this means that if you know that the molecule is at equilibrium with a given temperature, each time you measure it you can know, probabilistically, what the likelihood is that you will see it with a given energy.
*For completeness I will mention that some people have nevertheless tried to extend the idea of temperature to isolated systems, as the wiki mentions, but this temperature doesn't generally behave in the way you expect from open systems, and it isn't a very useful concept.
- 8,027
I think it is a mistake, as often happens in popularizations of science.
A water or any molecule may lose kinetic energy and acquire potential energy, but it is the kinetic energy distribution that gives the temperature of an ensemble of molecules. The shape of the distribution shows that there will always be individual molecules at very high energy, in the ensemble, which they acquire from the random individual collisions.
From the link,$$ f_{\varepsilon} \left(\varepsilon\right)\,\mathrm{d}\varepsilon ~=~\sqrt{\frac{1}{\varepsilon \pi kT}} \, \exp{\left(-\frac{\varepsilon}{kT}\right)}\,\mathrm{d}\varepsilon \,,$$and the shape shows that there always exist tails to high energies. The attribution of temperature labels to individual molecules is wrong.
Maxwell–Boltzmann probability density function, where $a=\sqrt{\frac{kT}{m}}$:
$\hspace{150px}$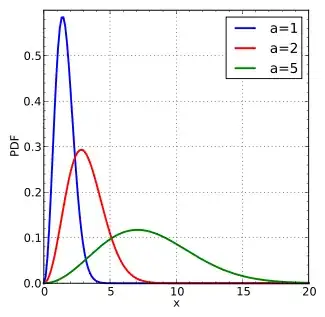 .
.
As the other answers have said, temperature is a collective property and can only be defined when you have an assemblage of particles. However by definition in a molecule you have an assemblage of atoms, and they have relative motions described by the vibrational excitations of the molecule.
So if you have a large enough molecule you can look at the excitations of its vibrational modes and use these to define a temperature. In effect what you're doing is saying that the excitation of the vibrational modes is the same as it would be if the molecule was in equilibrium with some enviroment of the defined temperature.
However I don't think this could usefully be applied to a water molecule. The vibrational excitations of water are of greater than thermal energy at ambient temperatures, and in any case there are only two normal modes. I suppose you could look at the rotation of the molecule, but this would give you only a rough guide to temperature.
- 367,598
It makes sense if all you know about the molecule is its expected energy. Then you can show that it's energy distribution is the Boltzmann distribution $p(E) = e^{-E/kT}$ for some constant $T$, which is related to the expected energy.
So the question reduces to a philosophical view of probabilities. Does it make sense to assign probabilities to a deterministic system? If you accept probabilities as the reflection of your knowledge of the system rather than something intrinsic then it also makes sense to assign temperature to a single molecule.
- 1,584
I humbly disagree with the majority of the other answers here. It can be very useful and make lots of sense to talk about the temperature of a single particle. You just need to realize that it's not quite the same (although it's pretty darn close) as the temperature defined by physicists in typical statistical mechanics and thermal physics studies.
Professional atomic physicists regularly refer to the "temperature" of single atoms, ions and molecules. See, for example, the discussion in this article. It's clearly not a temperature in the exactly same sense as a gas of particles has a temperature, but it's a very useful concept none-the-less. Temperature is basically being used as a proxy for the mean kinetic energy and distribution of energies that a single particle has over repeated realizations of a given experiment. In many cases the distribution is very well-approximated by a thermal Maxwell-Boltzmann distribution, and so assigning the particle a temperature associated with that distribution makes a lot of sense.
- 2,146
- 12
- 15
Thermodynamics makes sense when you have large numbers of particles. For example, the second law of thermodynamics has an extremely low probability of being violated when you have Avogadro's number's worth of particles. However, if you have a very small number of particles, the second law will frequently be violated.
This comes up in nuclear physics, where we routinely deal with nuclei consisting of 50 or 100 or 200 particles. Yes, we do talk about the temperature of an individual nucleus, and it does make sense.
However, a single water molecule is only 3 atoms, and in a system that size, it's nonsense to talk about temperature. In giant molecules, I can easily imagine that you could have enough atoms to talk about the temperature of an individual molecule.
Full disclosure, this answer is based on a paper I recently published on this topic. The paper's title, "Defining the temperature of an isolated molecule," gives away that my answer is yes, we can define such a temperature.
Indeed, the concept of the temperature of an isolated molecule in a vacuum isn't new. It's been around for decades in fields such as astrophysics and molecular beam collisions (I give many references in the paper).
For instance, PAH (polycyclic aromatic hydrocarbons) were discovered in interstellar media in 1984 when K. Sellgren assigned certain near-IR features appearing in the spectrum of several nebulae to the "thermal emission from very small grains (radius 10 Å) which are briefly heated to ~1000 K by absorption of individual ultraviolet photons." Such grains turned out to be large PAH molecules.
To define the temperature, we must consider that an isolated molecule is a microcanonical system conserving total energy. (At least in the short term, as it slowly irradiates the energy excess as a black body.) Therefore, we work with microcanonical temperatures rather than conventional canonical temperatures. The main distinction is that the microcanonical temperature is a function $T\left(E\right)$ of the total energy $E$, while the canonical temperature is the opposite; the energy $E\left(T\right)$ is a function of the temperature.
The problem of defining the microcanonical temperature of an isolated molecule boils down to whether it's possible to compute $$ T={{\left( \frac{\partial S}{\partial E} \right)}^{-1}} $$ for a finite system with a few degrees of freedom. In this equation, $S$ is the entropy, which, according to Boltzmann, is $$ {{S}_{B}}\left( E \right)={{k}_{B}}\ln \left[ \varepsilon \,\omega \left( E \right) \right],$$ where $ \omega\left( E \right) $ is the density of microstates with energy $E$.
In principle, the discrete nature of $E$ for a small, finite quantum system can pose significant troubles for computing the derivative defining the temperature. However, numerical tests show that as long the energy excess is not too small (near the zero-point level), $ \omega\left( E \right) $ is nicely differentiable.
Then, we can go on. We can compute $ \omega\left( E \right) $ for an isolated molecule numerically, get the derivative, and have its microcanonical temperature. If we are happy with a harmonic approximation for the normal vibrational modes, we can even get $ \omega\left( E \right) $ analytically and write a nice closed expression to $T\left(E\right)$.
We have just to consider another problem before: the entropy definition is not unique. According to Gibbs, for instance, the entropy should consider all microstates with energy small or equal to $E$, thus, it should be $$ {{S}_{G}}\left( E \right)={{k}_{B}}\ln \left[ \Omega \left( E \right) \right], $$ where $\Omega \left( E \right)$ is the integrated number of states.
Both entropy functionals in the thermodynamic limit give the same results for large systems. However, for a small, finite system such as an isolated molecule, the predictions from both approaches may not match. Indeed, this is the case for molecules up to about ten atoms.
Anyway, for a large molecule, Boltzmann and Gibbs volume microcanonical temperatures agree well. You can estimate them with this simple equation $$ T\left(E\right)={{\left[ \ln \left( \frac{E+{{E}_{ZP}}}{E-{{E}_{ZP}}} \right) \right]}^{-1}}\frac{2{{E}_{ZP}}}{N{{k}_{B}}}, $$ where $E_{ZP}$ is the harmonic zero-point energy and $N$ is the number of vibrational degrees of freedom $\left(N = 3N_{atoms}-6\right)$.
The figure below shows a few examples of the microcanonical temperature of isolated molecules in the harmonic approximation.
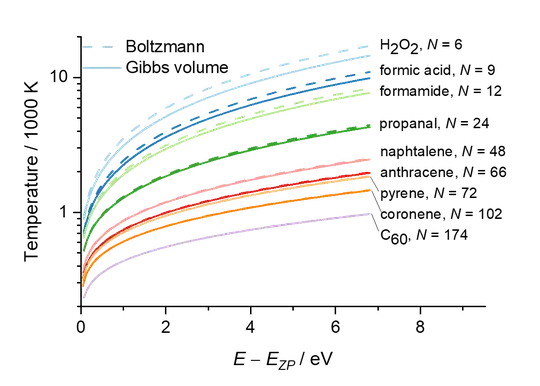
- 51
- 6
Temperature is a statistical phenomenon. So it only makes sense to apply it when statistics apply. In some sense, a single atom is "too small in number" to apply statistics to. However, there are more than one approaches to statistics. The above description is a frequentists phrasing. In a Baysean sense, it can be valid. You may model your knowledge of the kinetic energy of the particle using a random variable with some distribution. Naturally, a good distribution to use would be the distributions we use for temperature.
- 53,814
- 6
- 103
- 176
I will explain in simple....
We can measure temperature changes when a Source release energy or extract energy.
We know that every thing want to attain equilibrium. Therefore there should be an equality in temperature in all the atoms or molecules of a system.
The temperature of an atom will be same as that of temperature of surrounding.
But a thermometer is an external source of energy from surrounding. So it provides or extract energy from source.
Now Consider an $Ideal$ condition
Consider a atom placed in space and is away from every radiation from space and any atoms or any other gravity or electromagnetic forces.
Then the temperature will be $zero(Kelvin)$ theoretically and you cannot measure it experimentally !!
- 579
As stated in the other answers, in the specific scenario depicted in your question, it makes no sense to talk about the temperature of a molecule. But I can't help to widen the picture because there is a very interesting case here: what about the internal degrees of freedom of the molecule? So far everybody has only considered the motion of the whole molecule, because that was the context you implicitly gave, fair enough.
But what about the vibration of the molecular bonds? The rotations of two neighbour parts of the molecule about a bond? This is not as trivial! For small molecules, the number of associated degrees of freedom are too few to warrant talking about temperature. But it is not so for a large protein. There are so many of them that a statistical approach is possible: one can define an entropy, in the usual $\sum p\log p$ way, where $p$ is the probability for a given configuration. Then, as usual, if we have an entropy we can minimise it with the constraint of a given total energy, and a temperature comes out of that.
After writing this, I realised that @Rococo and @JohnRennie had written an answer on a similar line long before mine!