What is the temperature of a single proton?

Question

As it is said in general classical statistical mechanics, that temperature is nothing but just an integrating factor and T($E_{avg}$). And as proton is not a fundamental particle rather have inner structure is it okay to ask for temperature of a single proton (in deep space, with no electromagnetic interaction, gravity nothing)?

Answer 1

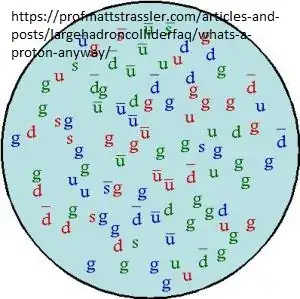
The proton is a bag of bound by color forces valence quarks and a sea of quark antiquarks and gluons, in the usual representation:

It is reasonable to ask whether a temperature can be defined, and yes, in the lattice QCD solutions there is a variable called temperature. Here is another paper..

The quark gluon plasma does have a temperature, and so in the cosmological models the formation of nucleons will have a transition temperature, from plasma to bound quarks.

There exists a QCD matter article in the wikipedia, which is relevant:

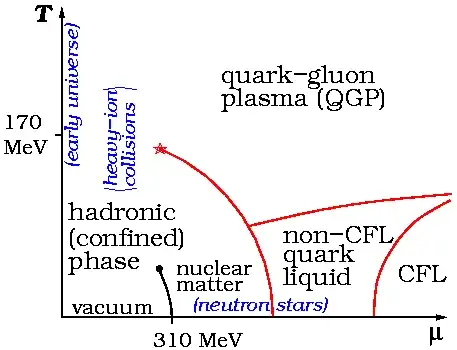
Conjectured form of the phase diagram of QCD matter, with temperature as ordinate (in mega-electron volts) and quark chemical potential as abscissa.

It is still a matter of research.

Answer 2

We can define temperature as $T$ the parameter of the Boltzmann distribution:

$$ p_i = \frac{1}{Z} e^{-E_i/kT} $$

With $p_i$ being the probability to have the system in a state with energy $E_i$.
And $Z$ being the normalization constant.

Now, under "a proton" we usually mean a system of three $uud$ valent quarks plus the surrounding excitation of the quark-gluon fields -- all in the ground (lowest energy) state. Since our definition restricts us to ground state only, we have $p_0 = 1$ and $p_i=0$ for $i>0$. Which for the Boltzmann distribution means $T=0$.

So, the formal answer to your question is $T=0$.

If you are interested whether it is possible to have the system of three $uud$ valent quarks plus the surrounding excitation of the quark-gluon fields in some non-groun state -- check the Delta barion.

Answer 3

There is no heat radiation bound in the force field of proton; the quarks inside proton possess some different radiations