The conceptual key here is that time dilation is not something that happens to the infalling matter. Gravitational time dilation, like special-relativistic time dilation, is not a physical process but a difference between observers. When we say that there is infinite time dilation at the event horizon we don't mean that something dramatic happens there. Instead we mean that something dramatic appears to happen according to an observer infinitely far away. An observer in a spacesuit who falls through the event horizon doesn't experience anything special there, sees her own wristwatch continue to run normally, and does not take infinite time on her own clock to get to the horizon and pass on through. Once she passes through the horizon, she only takes a finite amount of clock time to reach the singularity and be annihilated. (In fact, this ending of observers' world-lines after a finite amount of their own clock time, called geodesic incompleteness, is a common way of defining the concept of a singularity.)
When we say that a distant observer never sees matter hit the event horizon, the word "sees" implies receiving an optical signal. It's then obvious as a matter of definition that the observer never "sees" this happen, because the definition of a horizon is that it's the boundary of a region from which we can never see a signal.
People who are bothered by these issues often acknowledge the external unobservability of matter passing through the horizon, and then want to pass from this to questions like, "Does that mean the black hole never really forms?" This presupposes that a distant observer has a uniquely defined notion of simultaneity that applies to a region of space stretching from their own position to the interior of the black hole, so that they can say what's going on inside the black hole "now." But the notion of simultaneity in GR is even more limited than its counterpart in SR. Not only is simultaneity in GR observer-dependent, as in SR, but it is also local rather than global.
Is there a connected solution of 3+1 dimensional general relativity with one space-like slice not have a singularity, and another space-like slice having one.
This is a sophisticated formulation, but I don't think it succeeds in getting around the fundamental limitations of GR's notion of "now." Figure 1 is a Penrose diagram for a spacetime that contains a black hole formed by gravitational collapse of a cloud of dust.[Seahra 2006]

On this type of diagram, light cones look just like they would on a normal spacetime diagram of Minkowski space, but distance scales are highly distorted. The upright line on the left represents an axis of spherical symmetry, so that the 1+1-dimensional diagram represents 3+1 dimensions. The quadrilateral on the bottom right represents the entire spacetime outside the horizon, with the distortion fitting this entire infinite region into that finite area on the page. Despite the distortion, the diagram shows lightlike surfaces as 45-degree diagonals, so that's what the event horizon looks like. The triangle is the spacetime inside the event horizon. The dashed line is the singularity, which is spacelike. The green shape is the collapsing cloud of dust, and the only reason it looks smaller at early times is the distortion of the scales; it's really collapsing the whole time, not expanding and then recontracting.

In figure 2, E is an event on the world-line of an observer. The red spacelike slice is one possible "now" for this observer. According to this slice, no dust particle has ever fallen in and reached the singularity; every such particle has a world-line that intersects the red slice, and therefore it's still on its way in.
The blue spacelike slice is another possible "now" for the same observer at the same time. According to this definition of "now," none of the dust particles exists anymore. (None of them intersect the blue slice.) Therefore they have all already hit the singularity.
If this was SR, then we could decide whether red or blue was the correct notion of simultaneity for the observer, based on the observer's state of motion. But in GR, this only works locally (which is why I made the red and blue slices coincide near E). There is no well-defined way of deciding whether red or blue is the correct way of extending this notion of simultaneity globally.
So the literal answer to the quoted part of the question is yes, but I think it should be clear that this doesn't establish whether infalling matter has "already" hit the singularity at some "now" for a distant observer.
Although it may seem strange that we can't say whether the singularity has "already" formed according to a distant observer, this is really just an inevitable result of the fact that the singularity is spacelike. The same thing happens in the case of a Schwarzschild spacetime, which we think of as a description of an eternal black hole, i.e., one that has always existed and always will. On the similar Penrose diagram for an eternal black hole, we can still draw a spacelike surface like the red one, representing a definition of "now" such that the singularity doesn't exist yet.
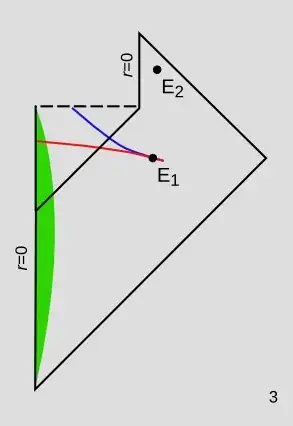
Figure 3 shows the situation if we take into account black hole evaporation. For the observer at event E$_1$, we still have spacelike surfaces like the blue one according to which the matter has "already" hit the singularity, and others like the red according to which it hasn't. However, suppose the observer lives long enough to be at event E$_2$. There is no spacelike surface through E$_2$ that intersects the cloud of infalling dust. Therefore the observer can infer at this time that all the infalling matter has hit the singularity. This makes sense, of course, because the observer has seen the Hawking radiation begin and eventually cease, meaning that the black hole no longer exists and its history is over.
Seahra, "An introduction to black holes," http://www.math.unb.ca/~seahra/resources/notes/black_holes.pdf


