What if two twins flew off in opposite directions and were reunited in a perfectly symmetric way, would they have aged same?

Question

If No, well this can't be, as there is perfect symmetry, you can't tell one from the other.

If Yes, they had relative velocities all along, then their times must have dilated and somehow they must not agree with each other.

P.S I know I am wrong, please help me find out where.

P.P.S For all those who are marking this as a duplicate question of What is the proper way to explain the twin paradox?, I think this is not same as plain old twin paradox because its made symmetric and the essence of the question is not how do you solve twin paradox, instead it is why is this not like twin paradox?

Answer 1

Yes, the two twins (with the same there-and-back speeds) would, upon their reunion, have aged the same.

Here's a spacetime diagram on "rotated graph paper" that displays the symmetry of the travelers. (The rotated graph paper helps us draw the clock ticks along various observer worldlines.) You could use this diagram to support various ways (e.g. from the other given answers) to explain the result that these twins would age the same.

The travelers each have there-and-back speeds of $(3/5)c$.

I have displayed each observer's lines of simultaneity, just before and just after her turn-around events. These are associated with relative-simultaneity and time-dilation.

I have also displayed the periodic transmissions by the initially-forward twin, and the receptions by the initially-backward twin. This shows what the initially-backward twin would "see". These are associated with the Doppler effect. (You can draw the corresponding transmissions by the initially-backward twin.)

Answer 2

Yes. Once the twins reunited, they would discover that they had aged the same amount of time.

This assumes that the twins return to their initial location, and that their paths have the same shape with respect to that location, but in different directions.

This must be true, because an observer who remained behind at the fixed location must see the same amount of time pass for either twin, regardless of the direction that the particular twin initially left that location.

During the journey, each twin would see the other twin's clock change at varying rates, depending on their relative velocity. However, once the twins returned to their initial location, the clocks would show identical values.

The following illustration shows what happens from the point of view of the stationary observer who remains home, and the values that appear on the clocks when the twins leave and when they return. The exact numbers would depend on the speed of the twins relative to the stationary observer and the distance traveled.

Answer 3

Yes, they would. Symmetry applies.

Suppose they start together at $t=0$ going with relative speed $v={3 \over 5} c$, (so $\gamma=1.25$) in opposite directions for a pre-agreed 5 days (each by their own clock). Each would say that when they did so, their twin's clock was running slow by a factor of 4/5.

Then they both slow down and reverse their direction of travel: we can assume this takes no significant time. When the stress of turnaround is over, they will each say that although their own clock is still showing 5, their twin's clock has jumped from 4 to 6.

The return journey takes 5 days, during which their twins clock runs slow again adding only 4 days, so both show 10 days at the end.

As always "A says B's clock shows $t_1$ when their own says $t_2$" means "A receives a picture of B's clock, showing $t_1$, at some time $t_3$: they correct for the transit time $\Delta$ and report $t_2=t_3-\Delta$. If the separation distance when the signal arrives is $X$ then $c\Delta=X+v\Delta$. On changeover the sign of $v$ changes, causing the jump in their evaluation of their twin's clock measurements.

The nice thing about relativity paradoxes is that they always have an answer.

Answer 4

1. yes they would have aged the same

2. you are saying if yes, then their times must have dilated and they must not agree

3. but what you are missing is that it is not speed that counts, because speed is symmetrically relative, but what matters is acceleration, because that is absolute

4. if they travel with constant speeds, then they only age less compared to the third twin (lets say there is a third twin on Earth) on Earth when they must decelerate at the point of return

5. that is the moment when because of deceleration (which is the same effect as gravity) the twins on the spaceships slow down in the time dimension

6. their four speed vector's magnitude must stay c, and if their spatial speed decelerates, their speed in the time dimension must slow down to compensate for the change in their spatial speed

7. so at the point of turn, they slow down in the time dimension compared to the third twin, and they age less, and the third twin ages more

8. but the two twins on the spaceships undergo acceleration/deceleration the same way symmetrically so their speed in the time dimension is the same, so they do not age compared to each other

Answer 5

Here's another way of thinking about it that might be helpful.

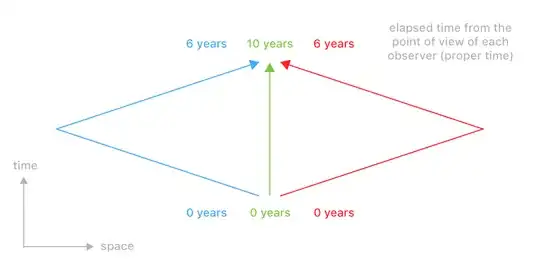
For the classical twin paradox, twin A is at rest and twin B travels away and comes back.

Imagine that each twin measures time using a "light clock", which is a pair of mirrors with a photon bouncing back and forth between them. Each time a mirror is stuck by a photon, this is interpreted as a tick of the clock.

In the following diagram, space is on the horizontal axis, and time is on the vertical axis.

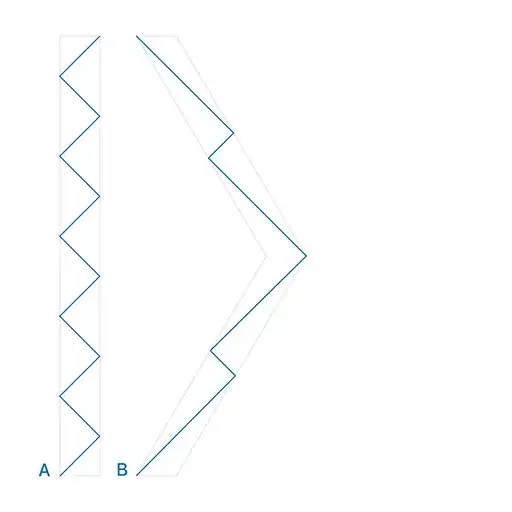
The blue lines are the paths of photons bouncing between the mirrors, which are the vertical or angled gray lines. Because the mirrors for twin B are moving at a significant fraction of the speed of light, it takes longer for the photon moving in the direction of the mirrors to catch up with them, and consequently the ticks are farther apart.

Twin A would observe that twin B's ticks are spaced farther apart, and therefore that twin B's time seems to be passing more slowly. However, twin B, traveling along with his clock, would always see the ticks happening at what he perceived as normal speed, since the clock would, by definition, measure the rate at which time was passing for him.

When twins A and B meet when twin B returns from his journey, twin A has counted 11 ticks, and twin B has counted 6 ticks.

For the extended twin paradox problem that you proposed, a third twin, C, would travel to the left of twin A and back, with a path otherwise identical to twin B. Twin C would also therefore count 6 ticks.

What if there was no stationary twin A, and just the two moving twins, B and C? They would still count 6 ticks each.

Using this kind of presentation, just concentrate on the paths of the photons between the mirrors and how many ticks of time are experienced by each of the twins.

What do you think of that way of thinking about it?