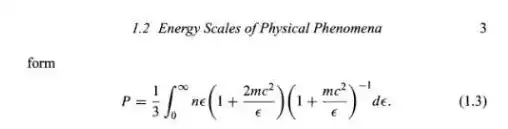0

I was studying a book called Theoretical Astrophysics by Prof T Padmanavan, and in the very first chapter, i find the expression of Net Contributing Pressure ($P$) as:

$$P = \frac{1}{3} \int_{0}^{\infty}n(\epsilon)p(\epsilon)v(\epsilon)d\epsilon$$

followed by relativistic momentum $P = \gamma mv$ and kinetic energy, $\epsilon = (\gamma-1)mc^2$ with $\gamma$ as the relativistic factor. By far this I understood it, but then, substituting these values in the above given expression, as:

$$P = \frac{1}{3} \int_{0}^{\infty}n\epsilon\left(1+\frac{2mc^2}{\epsilon}\right)\left(1+\frac{mc^2}{\epsilon}\right)^{-1}d\epsilon$$

is not understood by me. Can anyone please help me out with proper steps to achieve this expression. Thanks in advance !

enter image description here enter image description here

StephenG - Help Ukraine
  • 10,129
prikarsartam
  • 148

3 Answers3

2

Here are some useful relations for relativistic kinetic energy

$E=m\cosh\theta=m(\cosh\theta-1)+m= T+m $

$p=m\sinh\theta=m\sqrt{\cosh^2\theta-1}=\sqrt{m^2(\cosh\theta-1)(\cosh\theta+1)}=\sqrt{T(T+2m)}$

$m=\sqrt{E^2-p^2}$

$v=\tanh\theta=\displaystyle\frac{p}{E}=\frac{\sqrt{T(T+2m)}}{T+m}$

from my post https://physics.stackexchange.com/a/551250/148184

robphy
  • 12,829
1

First from the second identity, let solve it in terms of $\epsilon$ and generate some other useful equations:

$$\gamma-1=\frac{\epsilon}{mc^{2}}\quad\gamma+1=\frac{\epsilon}{mc^{2}}+2$$

$$\frac{\gamma+1}{\gamma-1}=1+2\frac{mc^{2}}{\epsilon}$$

$$\frac{\gamma-1}{\gamma}=\frac{\frac{\epsilon}{mc^{2}}}{\frac{\epsilon}{mc^{2}}+1}=\left(1+\frac{mc^{2}}{\epsilon}\right)^{-1}$$

So now notice, if we substitute $p$ into the integral (ignoring arguments, assumed to be $\epsilon$) we get:

$$P=\frac{1}{3}\int_{0}^{\infty}n\gamma mv^{2}d\epsilon$$

which depends on the square of $v$. We solve the third identity for $v^2$ in term of $\gamma$:

$$v^{2}=c^{2}\left(1-\frac{1}{\gamma^{2}}\right)$$

Now we can solve for the term inside the integral, which gives: $$\begin{aligned} \gamma mv^{2} &=\gamma mc^{2}\left(1-\frac{1}{\gamma^{2}}\right) \\ &=\gamma^{-1}mc^{2}\left(\gamma^{2}-1\right) \\ &=\epsilon\left(1+\frac{mc^{2}}{\epsilon}\right)^{-1}\left(1+2\frac{mc^{2}} {\epsilon}\right) \end{aligned} $$ where in the last step the previously determined identities were used: $$\begin{aligned} \gamma^{-1}\left(\gamma^{2}-1\right) &=\gamma^{-1}\left(\gamma-1\right)\left(\gamma+1\right)\\ &=\left(\gamma-1\right)\left(\frac{\gamma-1}{\gamma}\right)\left(\frac{\gamma+1}{\gamma-1}\right)\\ &=\frac{\epsilon}{mc^{2}}\left(1+\frac{mc^{2}}{\epsilon}\right)^{-1}\left(1+2\frac{mc^{2}}{\epsilon}\right) \end{aligned}$$ Substituting this result into the integral gives the form of the integral found in the book.

nluigi
  • 3,477
0

Thanks to @robphy for providing the answer, and with some algebraic manipulation, I got this:

$$P = \frac{1}{3}\int_{0}^{\infty}np(\epsilon)v(\epsilon)d\epsilon$$ $$= \frac{1}{3}\int_{0}^{\infty}np\frac{p}{\epsilon+m}d\epsilon$$

As, $v(\epsilon) = \frac{p}{E} = \frac{\sqrt{\epsilon(\epsilon+2m)}}{\epsilon+m}$ $$= \frac{1}{3}\int_{0}^{\infty}n\frac{p^2}{\epsilon+m}d\epsilon$$ $$= \frac{1}{3}\int_{0}^{\infty}n\frac{\epsilon(\epsilon+2m)}{\epsilon+m}d\epsilon$$

As, $p=\sqrt{\epsilon(\epsilon+2m)}$

Upto this, it was normalized as $c=1$, and reconsidering that, we get:

$$P = \frac{1}{3}\int_{0}^{\infty}n\frac{\epsilon(\epsilon+2mc^2)}{\epsilon+mc^2}d\epsilon$$ $$= \frac{1}{3}\int_{0}^{\infty}n\epsilon(1+\frac{2mc^2}{\epsilon})(\frac{\epsilon}{{\epsilon+mc^2}})d\epsilon$$ $$= \frac{1}{3}\int_{0}^{\infty}n\epsilon(1+\frac{2mc^2}{\epsilon})(\frac{1}{1+\frac{mc^2}{\epsilon}})d\epsilon$$ $$\therefore P = \frac{1}{3}\int_{0}^{\infty}n\epsilon(1+\frac{2mc^2}{\epsilon})(1+\frac{mc^2}{\epsilon})^{-1}d\epsilon$$

prikarsartam
  • 148