What do spacelike, timelike and lightlike spacetime interval really mean?

Question

Suppose we have two events $(x_1,y_1,z_1,t_1)$ and $(x_2,y_2,z_2,t_2)$. Then we can define

$$\Delta s^2 = -(c\Delta t)^2 + \Delta x^2 + \Delta y^2 + \Delta z^2,$$

which is called the spacetime interval. The first event occurs at the point with coordinates $(x_1,y_1,z_1)$ and the second at the point with coordinates $(x_2,y_2,z_2)$ which implies that the quantity

$$r^2 = \Delta x^2+\Delta y^2+\Delta z^2$$

is the square of the separation between the points where the events occur. In that case the spacetime interval becomes $\Delta s^2 = r^2 - c^2\Delta t^2$. The first event occurs at time $t_1$ and the second at time $t_2$ so that $c\Delta t$ is the distance light travels on that interval of time.

In that case, $\Delta s^2$ seems to be comparing the distance light travels between the occurrence of the events with their spatial separation. We now have the following definitions:

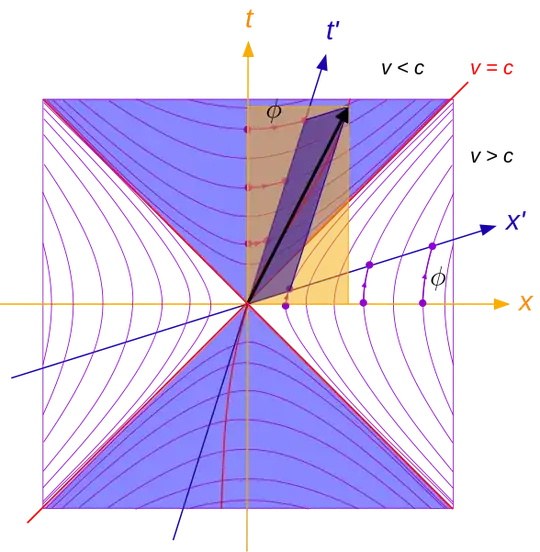
• If $\Delta s^2 <0$, then $r^2 < c^2\Delta t^2$ and the spatial separation is less than the distance light travels and the interval is called timelike.

• If $\Delta s^2 = 0$, then $r^2 = c^2\Delta t^2$ and the spatial separation is equal to the distance light travels and the interval is called lightlike.

• If $\Delta s^2 >0$, then $r^2 > c^2\Delta t^2$ and the spatial separation is greater than the distance light travels and the interval is called spacelike.

These are just mathematical definitions. What, however, is the physical intuition behind them? What does an interval being timelike, lightlike or spacelike mean?

Answer 1

Let's suppress some dimensions to simplify:

$$\Delta s^2 = -(c\Delta t)^2 + \Delta x^2 $$

This quantity $$\Delta s^2$$ is preserved by changes of reference frame, just as in Galilean physics the quantity $$\Delta r^2 = \Delta x^2 + \Delta y^2 $$ is preserved by rotations.

Notice it is also the equation of a hyperbola. Thus, the effect of a frame shift is to slide events around on hyperbolae of constant $\Delta s^2$.

Here's a helpful image from Wikipedia (attribution below):

Ignore the vectors and just look at the hyperbolae. Events on a given hyperbola must, under a given frame boost, remain on that hyperbola.

Now you might notice those hyperbolae seem to come in two classes, those on the top and those on the bottom. The "v=c" hyperbolae - the straight lines - divide the two. Events on those are said to be "lightlike (or null) separated from the origin". Notice that for these, $\Delta s^2$ is just zero.

The hyperbolae in the purple regions are said to be timelike separated from the origin. This is because no matter how much they slide around on their hyperbolae, their ordering compared to the origin never changes. Any events in the purple regions which occur before (after) the origin will occur before (after) the origin to all observers. Thus, this set of events - plus the null events - is said to be causally connected with the origin. The fact that the ordering of these events with the origin in time is fixed motivates the term.

The hyperbolae in the white regions do not have this property. Some observers think they happened before O, while some think they happened after. It had therefore better be true that nothing about O depend logically on happening after (or before) these events! Otherwise we could break logic by running really fast.

However, notice that it is not possible to slide the white-region events from one side of the origin to the other. This makes the separation more like our normal ideal of "distance", so we say the events are spacelike separated.

Image attribution: "Minkowski lightcone lorentztransform" by Maschen - Own work. Licensed under Public Domain via Commons

Answer 2

Spacelike separation means that there exists a reference frame where the two events occur simultaneously, but in different places. Timelike separation means that there exists a reference frame where the two events occur at the same place, but at different times. Lightlike means that, well, light could travel between those points.

Answer 3

Let's put it very simple: They tell you "how far something is apart compared to c"

time-like: if you are fast enough, you can be at (think spatial, like "at the festival") event a and at event b, it is only a "matter of time" until you see the second event

space-like: the two events are too far apart (in space). You cannot see both of them together, no matter how fast you are. As soon as event a happened and you go as fast as possible, event b will have happened before you arrive there.

light-like: exactly in between, the events are so far away that if you are as fast as light, you can see both events. If they are further away, they become space-like, if they are closer they become time-like

So a space-like separation makes any causal relation between the two events impossible, i.e. one cannot cause or influence the other.$^1$

1) as mentioned, a common cause (an event that is time-like to both events) can still make the two correlated.

Answer 4

Timelike is when an event is inside the lightcone (as you have mentioned) and as a result, one event CAN affect the other event (there can exist a causality between the two events. E.g. lets say there are two events, where I shoot a laser and another event where someone gets hit by a laser. If they are timelike seperated then the laser that hit the dud could have been from me).

Spacelike is when the two events are outside lightcone (as you have also mentioned) and as a result, one event CANNOT affect the other event. (For the previous example, it is impossible that my laser hit the dude and killed him, so I can safely conclude that someone else shot the laser to kill him.)

Lightlike is a special case which is like inbetween the two. For me to kill him, all the interval inside must have been vaccuum.

Answer 5

spacelike, timelike and lightlike [...] What, however, is the physical intuition behind?

Using "physical" terminology means (foremost, and even exclusively) to refer to distinguishable "participants" (a.k.a. "principal identifiable points", or "material points") where

• each is (thought as being) capable, at least in principle, of determining with whom they had been coincident ("meeting at an event"), and with whom not, and in which sequence one had taken part in different concidence events, and

• each is (thought as being) capable, at least in principle, of observing and recognizing others in their distinguishable states (having taken part in particular coincidence events, having collected certain observations), thus exchanging signals between each other (i.e. especially referring to one's first observation of a given signal state).

In this terminology, any one event is characterized by who had taken part, and by which signals (of other events) the participants first observed at this coincidence occasion.

The relation between two distinct given events may accordingly be characterized as follows:

• either all participants in one event had thereby first observed the (signals of) the other event. Such pairs of events are conventionally characterized by a null interval,

• or else at least one identifiable participant having taken part in both events (or at least being thought as having taken part in both events). Considering three or more such events they are conventionally assigned suitably generalized metric relations between each other to satisfy the inverse triangle inequality,

• or neither. Metric relations assigned to three or more such events may or may not satisfy the triangle inequality.

However, as technical terms, the words "spacelike, timelike and lightlike" require some (not quite arbitrary) additional assignment of coordinates to a given set of events, in order to describe their relation as elements of a Lorentzian manifold.

Answer 6

Consider an interval from event a to event b:

• The interval is time-like if it large in time but small in space. If you are at event a, you have enough time to get to event b. Event a can directly influence event b, and all observers will agree that event a happened before event b. (Think "the change in time is greater than the change in space.")

• The interval is space-like if it is large in space but small in time. If you are at event a, there's no way to move quickly enough to get to event b. Event a cannot directly influence event b, and observers may disagree as to which event occurred first. (Think "the change in space is greater than the change in time.")

• The interval is light-like if it is as large in space as it is in time (relative to c). (Think "the change in time equals the change in space.")

If a light-like interval moves further apart in space or closer in time it becomes space-like; if it moves further apart in time or closer in space it becomes time-like.

(This answer is a rewrite of Mayou36's.)

Answer 7

In the context of different spacetimes and not spacetime intervals within the same spacetime. The definition could be extended as following:

Simply put, time-like or light-like is our known spacetime where causality is dictated by the speed of light. Thus for example, light-like in the vacuum where the speed of light is $c$ and time-like inside a transparent medium like glass where the speed of light is lower than $c$.

Space-like is a hypothetical spacetime where causality is dictated by faster than light FTL speed limit and when projected in our time-like or light-like spacetime this could even resemble to "Instantaneous action at a distance" or else known by famous Einstein as "Spooky action at a distance".

However, such a spacetime domain has not yet being discovered within our cosmos and therefore not regarded today as a possible explanation for the observed Quantum Entanglement phenomena.

Nevertheless, Dark Energy seems to have a space-like spacetime behavior.