Time-like separated and Space-like separated events

Question

I am trying to get an intuition about Time-like separated and Space-like separated events. I understand the definition of these terms, but I lack intuitive understanding of what these concepts actually mean :)

Why are they called this way?

Answer 1

Since you mention in your comment that you're familiar with the definition of the spacetime interval:

$$\Delta s^2 = -c^2\Delta t^2 + \Delta \vec{r}^{\ 2}$$

(I'm taking $\Delta \vec{r}$ as $\Delta \vec{r}=(\Delta x,\Delta y,\Delta z)$ for brevity).

Then you know from the definitions that:

1. $\Delta s^2 < 0$: correspond to a time-like pair of events
2. $\Delta s^2 > 0$: correspond to a space-like pair of events
3. $\Delta s^2 = 0$: correspond to a light-like pair of events

The reason for these names is that for example with a time-like pair, the time component $c^2\Delta t^2$ is larger than the spatial component $\Delta \vec{r}^{\ 2}$. Hence making the combination $-c^2\Delta t^2 + \Delta \vec{r}^{\ 2}$ negative. You can think of such a pair of events as having "more time than space" between them.

Likewise, the spatial component $\Delta \vec{r}^{\ 2}$ is larger than $c^2\Delta t^2$ for space like events, there is "more space than time" between such two events.

Finally when $c^2\Delta t^2=\Delta \vec{r}^2$ the events are light-like, they physically correspond to the motion of light (at least in flat spacetime, which is what special relativity deals with).

---

Now, having laid this groundwork, you can intuitively think about these two (or three, if you include light-like pairs) types of event pairs in terms of causality.

Time-like pairs can be causally related because they correspond to two events that can be related by an influence that propagates from one event to the other with a velocity that's less than that of light.

To see that, we use the above definition for time-like separation to write:

$$ \Delta s^2 = -c^2\Delta t^2 + \Delta \vec{r}^2 < 0 $$

$$\frac{\Delta \vec{r}^{\ 2}}{\Delta t^2} < c^2 $$

Which shows that, for example, it's possible for a particle to move along the spatial interval $\Delta \vec{r}$ during the time interval $\Delta t$ with a speed strictly less than $c$.

An example of a pair of time-like events is a person waking up at morning and the same person going to bed at night. In fact, any two events along the worldline of any massive particle must be time-like separated, because massive particles can't exceed the speed of light, just as the person didn't exceed the speed of light between waking up and going to bed again.

Similarly, by applying exactly the same argument to space-like events one finds:

$$\frac{\Delta \vec{r}^{\ 2}}{\Delta t^2} > c^2 $$

So such pairs of events can't be causally related, since according to our current knowledge no influence can propagate faster than light. An example of such a pair of events is two different people waking up simultaneously at exactly 8:00AM. You can find a frame of reference where one wakes before the other, but since in all frames, by the invariance of the interval you get $\Delta s^2 > 0$, the events can't be causally related.

Finally, the in-between case of $\Delta s^2=0$ simply corresponds to the motion of light rays:

$$ |\Delta \vec r| = c|\Delta t| $$

A few additional notes

1. You are likely to encounter the terms "time-like" and "space-like" in additional contexts apart from referring to pairs of events. For example, we say that the four velocity is a "time-like" four vector because for any four velocity $\mathbf{u}$ we have $\mathbf{u}\cdot\mathbf{u} = -c^2 < 0$. Similarly the four acceleration $\mathbf{a}$ is space-like: $\mathbf{a}\cdot\mathbf{a} = \alpha^2$ where $\alpha$ is the proper acceleration.

2. It's a nice exercise to prove to yourself that if two events are time-like, there's always a frame where they happen at the same point in space, and that there is no frame where they happen at the same time. Likewise, one can prove that if two events are space-like there's always a frame where they are simultaneous, but no frame where they happen at the same point in space. One can do that either algebraically by using the Lorentz transformations, or by using a spacetime diagram and geometrical arguments. It's best to do both in my opinion; these are such fundamental concepts, hence I think it's good to learn more than one way to think about them.

3. Everywhere in my answer here I've used the metric convention denoted by $(-+++)$, also known as the "mostly pluses" metric signature. The only effect of using one and not the other is to reverse the definition of time-like and space-like in relation to the sign of $\Delta s^2$, so you need to beware that different books/sources can use the other convention.

Finally, it would be amiss of me to neglect to mention in such a post the intuition to be gained by looking at spacetime diagrams such as this one:

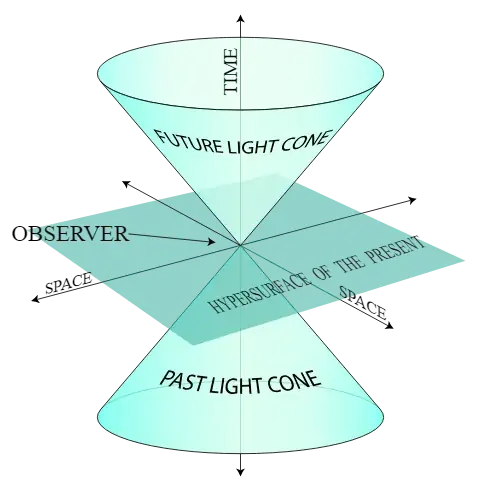
^{This diagram is from https://en.wikipedia.org/wiki/Light_cone}

If you use units in which $c=1$, neglect one of the spatial dimensions and draw the worldline of a light ray from your current location, what you will get is this kind of diagram. What you're seeing is that the light ray is describing a cone that is at $45^{o}$ angle relative to the spatial plane (this is due to having $c=1$).

You can imagine the spatial dimensions $(x,y)$ to correspond to the two axes denoted "space" in the diagram, and $t$ to time of course.

If you imagine yourself being at the origin, everything within the light cone centered on you are events that are in a time-like relation to you. As a pair your event of "now" and such an event within the light cone, are time-like. Similarly, anything outside this light cone is space-like in relation to your "now".

The geometric picture of special relativity is something worth getting familiar with. You can gain more insight into it, for example from this page -- credit to Rob Salgado, who happens to be a member of this site, and often includes such great visualizations in his posts :)

Answer 2

Events are not time-like or space-like. Only intervals (or vectors) are.

Events are points in spacetime. Given two events, the interval between them is (1) time-like if some massive object could have both events on its world-line, i.e. there is a frame in which the events have the same spatial coordinates and differ only in time; (2) null if the events could be connected by a beam of light; and (3) space-like if there is a frame in which the two events happen at the same time. Mathematically these correspond to the possibilities for the sign of the spacetime interval.

You could (in principle) go between time-like separated events by slower than light travel. To go between space-like separated events would require faster than light travel.

Answer 3

tl dr answer:

For two events $E_1$ and $E_2$, if they are

TIMELIKE: there is a frame in which they occur at the same place, at different times.

SPACELIKE: there is a frame in which they are simultaneous; they occur at the same time in different places.

Edit: I meant my answer (a tl;dr) to supplement the other correct answers, but per the OP's request:

Consider events in $S$ labels as:

$$ E_i = (t_i, x_i)_S $$

For 2 events to occur at the same place, the space-coordinate is the same:

$$ E_0 = (0, 0)_S $$ $$ E_1 = (T, 0)_S $$

(there is no loss of generality by placing it at the origin). $E_1$ happens a time $T$ after $E_0$, in the same place.

In any moving ($v$) frame $S'$, then:

$$ E_0 = (0, 0)_{S'}$$ $$ E_1 = \big(\gamma T, -\gamma v T \big)$$

so they are no longer in the same place, and the time between them is shorter.

The invariant interval is:

$$ \Delta s^2 = c^2(E_{1, t}-E_{0, t})^2 -(E_{1, x}-E_{0, x})^2$$ $$ \Delta s^2 = \gamma^2 T^2 - (c^2 - v^2) = (cT)^2 > 0 $$

That's invertible, so if you start in $S'$, if $\Delta s^2 > 0$, you can always find a frame where the events are colocated.

For 2 events to occur at the same time, the time-coordinate is the same:

$$ E_0 = (0, 0)_S $$ $$ E_1 = (0, X)_S $$

(there is no loss of generality by placing it at the origin). $E_1$ happens a distance $X$ from $E_0$, at the same time.

In any moving ($v$) frame $S'$, then:

$$ E_0 = (0, 0)_{S'}$$ $$ E_1 = \big(-\gamma \frac{vX}{c^2}, \gamma X \big)$$

so they are no longer simultaneous, and the distance between them is longer.

The invariant interval is:

$$ \Delta s^2 = c^2(E_{1, t}-E_{0, t})^2 -(E_{1, x}-E_{0, x})^2$$ $$ \Delta s^2 = X^2 < 0 $$

That's invertible, so if you start in $S'$, if $\Delta s^2 < 0$, you can always find a frame where the events are simultaneous.

Note: I find that our Galilean intuition makes us want to assign a preferred frame to events, e.g. in Einstein's train/lightning event. If the bolts strike the ends of the train or if the bolts strike the ground next to the ends of the train, it's tempting to prefer that they belong to the train (station) frame, but that will lead you astray. (e.g, I've seen explanations where ppl say, "The train sees the lightning strike from a moving frame" so....", No! that is wrong. Events are just abstract points in spacetime, they don't move. An event is a moment in time, at a point in space, and has different coordinates in different frames.

Answer 4

Okay, let me give it a shot. Rather than define jargon terms:

A spacetime interval is just 4 dimensional distance. Unlike 3D distance, which changes depending how fast the observer is moving, 4D distance is absolute (Lorentz-invariant).

Time is just a direction you can move in, like up-down and left-right. Everything with mass moves in the past-future direction at c.

It's absolutely impossible for mass go backwards in time. Light can, but people in the past can't see it. 2 bad.

The only difference between elapsed time and a spatial distance is, an elapsed time "acts" like negative distance. In fact, according to Einstein's interval metric equation, that's exactly what it IS.

A spacetime interval is just the length of the 4D path of something that existed for a little while.

If that path took less space distance than it did time distance, then the object has mass. The jargon is, that interval is "timelike." Given enough time, you can get from here to there.

If the path took the same amount of distance in space as it did in time, then the object is a photon and it's traveling at c.

If an object got from here to there faster than the speed of light, then the space distance is greater than the time distance — a "spacelike" interval. Those intervals cannot occur in reality. [curtsies]