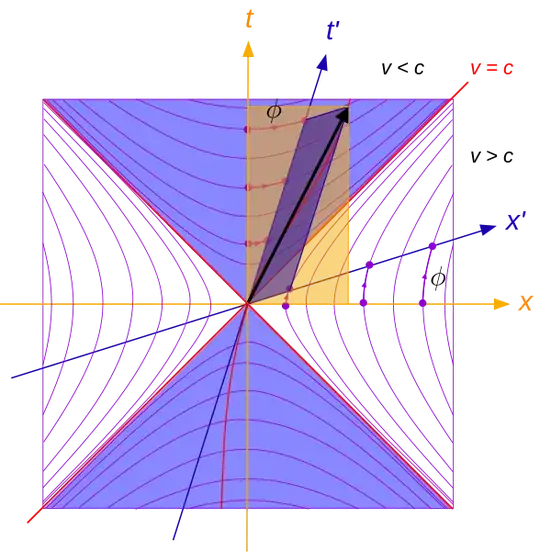
All points on a given hyperbola are separated from the origin by the same spacetime interval $\Delta s$. We can say that not only is $\Delta s$ frame invariant, so are the hyperbolas.
Let's suppose we have two events, A and B, with A at the origin, $x_A = 0$, $t_A = 0$; and B is at $x_B = 3.0$, $t_B = 5.0$. (Same units for $x$ and $t$. I'm using an example from Thomas A. Moore's book A Traveler's Guide to Spacetime.)
In the $x$-$t$ frame,
$$\left(\Delta s\right)^2 = \left(\Delta t\right)^2 - \left(\Delta x\right)^2 = \left(5.0\right)^2 - \left(3.0\right)^2 = \left(4.0\right)^2.$$
Now consider the $x'$-$t'$ frame, moving at some speed $v$ relative to the $x$-$t$ frame. We assume the $x$-$x'$ axes are parallel, and that the origins of the two frame overlap at event A. We have two options on how to represent the $x'$-$t'$ frame. The first, as shown in your figure, is to draw the $x'$-$t'$ axes on the same diagram with the $x$-$t$ axes. Obviously, nothing already drawn on the figure will change when the $x'$-$t'$ axes are added to the figure, including the hyperbolas and the positions on the figure of the spacetime points A and B.
We can use the hyperbolas to calibrate the scales on the $x'$ and $t'$ axes against the scales on the $x$-$t$ axes, and then we can identify the coordinates of A and B in $x'$-$t'$ system. Suppose that $v$ is such that we get $\Delta x' - 5.0$ and $\Delta t' = 6.4$. (As an exercise, you can work out the value of $v$ from these differences.)
Then, for the $x'$-$t'$ frame, we get
$$\left(\Delta s'\right)^2 = \left(\Delta t'\right)^2 - \left(\Delta x'\right)^2 = \left(6.4\right)^2 - \left(-5.0\right)^2 = \left(4.0\right)^2.$$
The second option is to redraw the figure with the $x'$-$t'$ axes in the normal orientation. The hyperbolas will not change at all because, like $\Delta s$, they are invariants. Neither will the position of event A since it is at the origin in both frames. But the position of event B must change because the $x'$-$t'$ axes are now drawn differently. Since $\Delta x' = -5$ event B will now 'hop' to the left side of the $t'$ axis on the new figure. But it will nevertheless fall onto the same hyperbola as on the original figure.
Why does B fall on the same hyperbola? Because a given hyperbola always represents all points at a common spacetime interval from the origin. Event B is separated from event A by the same $\Delta s$ in all inertial reference frames. It doesn't matter how the axes are drawn. So event B must fall onto precisely the same hyperbola when the figure is redrawn. In addition to hopping to the left of the $t'$ axis, event B has to move toward the top of the figure.
For any value of $v$, we will get $\left(\Delta s\right) = (4)^2.$ If we take event A to define the origin of all possible inertial frames moving with speed $v$ relative to the original $x$-$t$ frame, then event B must fall onto the same hyperbola in all inertial frames. And because the hyperbolas are themselves invariant, we can say B is falling onto literally the same hyperbola in all frames. Adjusting the value of $v$ will do one of two things to the figure, depending on which version of the figure we use.
For the original version, in your post, changing the value of $v$ does not shift the positions of the A and B events on the figure. It causes the $x'$-$t'$ axes to either close in on or open up from the $v = c$ axis. For the alternative version, where the $x'$-$t'$ axes are drawn in the normal orientation (so really we have a new alternative figure for each value of $v$), the point B will slide along $\left(\Delta s\right)^2 = \left(4\right)^2$ hyperbola. So it is in this sense that events can be 'moving' points on a spacetime diagram.
I think you're correct that saying the events 'move' is a little confusing. The events are not moving in a physical sense.
Hope this helps.