Adapted from "Quasicrystals: Definition and Structure", D. Levine and P. J. Steinhardt.
Traditionally, the structure of solid has been divided in two macro-categories: crystalline and amorphous solids.
Crystalline solids are characterized by long-ranged translational and rotational order, the latter corresponding to special discrete subgroups of the rotation group. Moreover, they have rotational point symmetry.
An amorphous structure, by contrast, lacks every kind of long-ranged order and only posses local ordering.
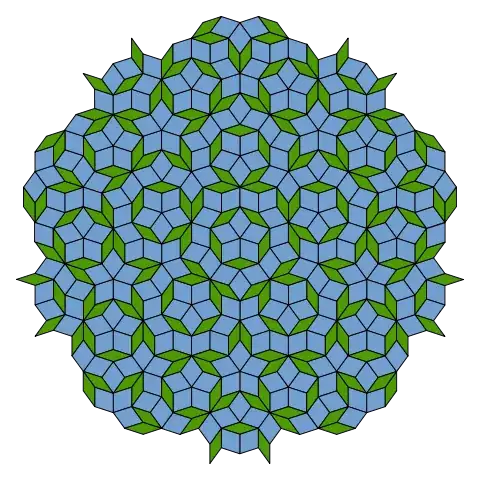
Quasicrystals are intermediate between crystals and amorphous solids in the sense that they possess long-ranged translational and orientational order, but this order is not periodic. Moreover, they lack a rotational point symmetry. We call such a structure quasiperiodic. An example is the famous Penrose tiling, which is shown in the following picture (source: Wikipedia).