A phase transition is a change in the nature of a phase or in the number of phases of a system as a result of a change in the external conditions. Examples: melting/freezing, vaporization/condensation, ferromagnetic transition, superconducting transition.
A phase transition is defined as
A change in the nature of a phase or in the number of phases as a result of some variation in externally imposed conditions, such as temperature, pressure, activity of a component or a magnetic, electric or stress field.
Everyday examples of phase transitions are the melting of ice and the evaporation of water. Other examples are the ferromagnetic transition in a magnetic solid, the superconducting transition in a superconductor and the nematic transition in a liquid crystal.
To every phase transition, we can associate an order parameter $\phi$, which is normally zero in the "ordered" phase and non-zero in the "disordered" phase. Examples of order parameters are
- $\Delta \rho=\rho_\text{liquid}-\rho_\text{gas}$ (condensation/evaporation)
- Spontaneous magnetization $\mathbf M$ (ferromagnetic)
- $\int d\mathbf x \langle \psi \rangle$ (superfluid)
To the order parameter are associated a thermodynamic potential $G$ (usually the free energy) and a conjugate field $H$:
$$\phi = -\frac{\partial G}{\partial H}$$
For example, in a ferromagnet the conjugate field of the magnetization is the external magnetic field $\mathbf h$.
If $\phi$ disappears continuously at the phase transition, we talk about first-order phase transition; if it disappears discontinuously, we talk about second-order (or continuous) phase transition.
The other derivative of the thermodynamic potential is the entropy:
$$S = -\frac{\partial G}{\partial T}$$
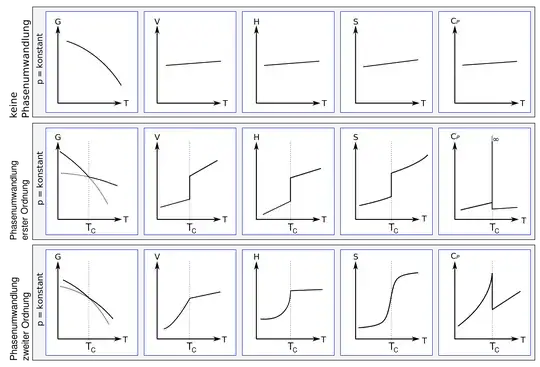
At first-order phase transition, entropy (and also volume and enthalpy) has a jump discontinuity, while at a second order phase transition it remains continuous, while its derivative changes discontinuously (Fig. 1).
Other relevant quantities are the susceptibility $\chi$ and the specific heat $C$:
$$\chi = -\frac{\partial^2 G}{\partial H^2}=\frac{\partial \phi}{\partial H}$$ $$C = -T \frac{\partial^2 G}{\partial T^2}$$
Fig. 1: The behavior of various thermodynamic quantities (Gibbs free energy $G$, volume $V$, enthalpy $H$, entropy $S$ and specific heat $C_P$) during a phase transition. First line: no phase transition. Second line: first-order phase transition. Third line: second-order phase transition. From Wikipedia.
Second-order phase transitions are characterized by a power-law singularities in the susceptibility and in the specific heat at the critical temperature $T_c$:
$$\chi \propto \left(1-\frac{T}{T_c}\right)^{-\gamma}$$
$$C \propto \left(1-\frac{T}{T_c}\right)^{-\alpha}$$
In addition, we have the relations
$$\phi \propto \left(1-\frac{T}{T_c}\right)^{\beta}$$
$$\phi \propto H^{1/\delta} \ \ \ (T=T_c)$$
The exponents $\alpha,\beta,\gamma,\delta$ are known as critical exponents. The following relations are valid in general:
$$\alpha+2\beta+\gamma=2 \ \ \ \text{(Rushbrooke identity)}$$ $$\gamma=\beta(\delta-1) \ \ \ \text{(Widom identity)}$$