I'm preparing for my exam, but I have difficulties in perceiving why there is a $\frac{1}{2}$ in the distance formula $d=\frac{1}{2}at^2$?
Asked
Active
Viewed 2,100 times
3 Answers
2
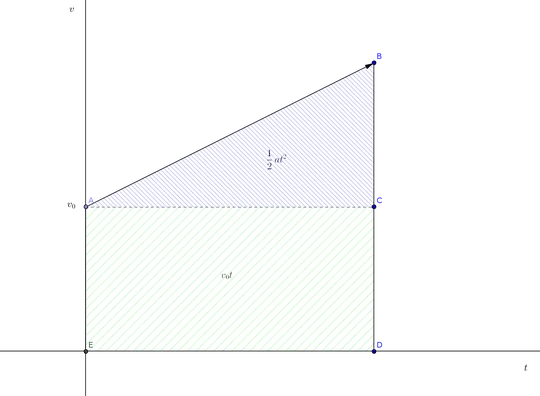
$\Delta x =v_{average}\times t$
In uniform acceleration $v_{average}$ becomes $\dfrac{v-v_{0}}{2}$
Hence;
$\Delta x =\dfrac{v-v_{0}}{2}t=\dfrac{1}{2}\dfrac{v-v_{0}}{t}t^{2}=\dfrac{1}{2}at^{2}$
N.G.Tyson
- 802
1
We can also do it using calculus,the displacement of the particle is given by
$$v=u+at$$
$$\rightarrow v\,dt = u\,dt + at\,dt$$
$$\rightarrow \int_0^t v\,dt = \int_0^t u\,dt + \int_0^t at\,dt$$
$$\rightarrow s = ut + \frac{1}{2}at^2$$
If $$u=0$$
$$\rightarrow s=\frac{1}{2}at^2$$
Chris
- 17,377