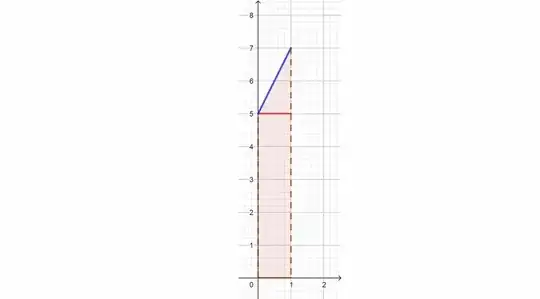
When you're moving at $5$ m/s for $1$ second, you have traveled $5$ m.
When you're moving at $5$ m/s (initial velocity) and you accelerate $2$ m/s for $1$ second, you have traveled $5$ m + $1$ m (distance traveled because of acceleration).
But does this hold true in real life? If I was to test this out, would the distance traveled because of acceleration equal $1$ m?
depending on the frame of reference, taking relativity into account, a stationary observer would say yes. to the object moving it would be minutely farther, as its second would be longer, according to the stationary meter+ traversed.
Let $y$-axis shows speed, and $x$-axis represents time:
The $\color{red}{\mathrm {red\ line}}$ is the graph for the first moving with $\color{red}{constant}$ speed, the $\color{blue}{\mathrm {blue\ one}}$ for your second (accelerated) moving with $\color{blue}{increasing}$ speed.
The area under them is the traveled distance, so you may see, that for the accelerated moving it's the sum of traveled distance for moving with constant speed plus area of the triangle over the rectangle, which is always $at/2$, giving in your case $2\cdot 1 / 2 = 2\cdot t / 2 = t=1$.
So in the more general case, when time may be other than $1$ s, but the acceleration is still $2\,\mathrm{ms^{-2}}$, it is true, but only numerically, that $s_2=s_1+t$.
