Pn junction voltage drop?

Question

This image from wikipedia, explains that there occurs a potential drop across a pn semiconductor junction, and an electric field confined to the depletion region.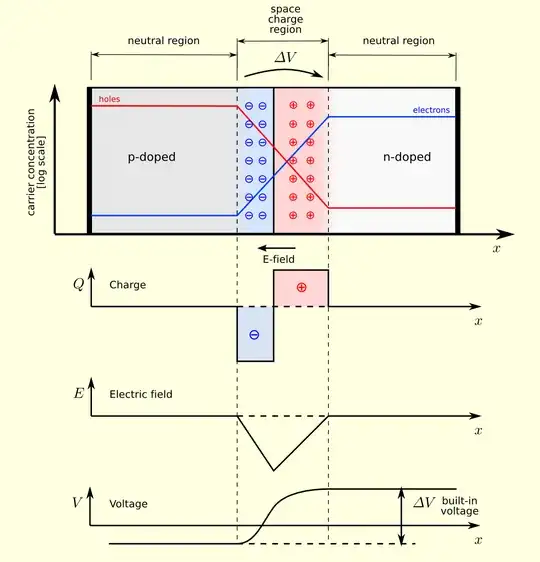

I already know the reason for the existence of this drop and the calculation of the difference but I have two questions regarding this drop.

1) If the n and p doped regions are externally connected using a perfectly conducting wire, why will not any current flow?
Connecting the two regions should equalize their potentials (since wire is a resistance less) conductor, and therefore the gradient at the junction is destroyed resulting in a diffusion current which is obviously against conservation of energy as the semiconductor has non-zero resistivity. Where will extra potential drops will be created so that Kirchoff's voltage rule holds without any current and the built-in potential difference $V_o$ of the juction persists?

2) (probably naive) If an external Bias is applied, of say $|V|<|V_o|$, then the pn potential difference across the junction will just reduce by that amount ($|V|$). Assuming that the external voltage source is ideal without any resistance, what will be the potential drops which would sum to zero in this case? Will drop due to the resistance of semiconductor play a par in it? If yes, then there cannot be any ideal resistance-less semiconductor junction, can there?

Answer 1

Calling it a built-in voltage is something of a misnomer. People usually think of "voltage" as "what you measure with a voltmeter". So "voltage" is normally synonymous with "electrochemical potential of electrons" (in stat mech terminology) and with "difference in fermi level" (in semiconductor terminology). Under this definition, the built-in "voltage" is not actually a voltage.

Then what is it? It's what chemists call "galvani potential", and some physicists call "electrostatic potential". It's the line-integral of electric field. (Maybe you should call it "built-in potential", not "built-in voltage".)

Voltage / fermi level measures the total "happiness" of electrons, the sum of all influences on the electron. The electric field (galvani potential) is just one of those many influences. Other influences include diffusion (entropy), the kinetic energy of the electron's wave function, etc. etc. But it's the sum of all influences that determines how the electron moves. That's why it is the voltage, not the galvani potential, that determines the most important things like current flow and energy dissipation.

So to summarize: The "voltage" across a p-n junction is zero, when the word "voltage" is defined in the most common and sensible and intuitive way. After all, the junction is in equilibrium; an electron is equally happy to be on either side.

For more details see my other answer: Fermi level alignment and electrochemical potential between two metals

Going around a loop, both the voltage differences and the galvani potential differences sum to zero. But only the former is really important. For the galvani potential differences, most of them are unobservable, like the volta potential at the junction when you solder an aluminum wire to a copper wire. It is possible to figure out the galvani potential differences everywhere in a p-n junction circuit, including at the wire contacts, at the voltmeter, and so on. If you do figure them out, and add them all up, you'll get zero! But since none of those parameters matter for the circuit behavior, people rarely think about them or try to figure them out.

Answer 2

1) If the n and p doped regions are externally connected using a perfectly conducting wire, why will not any current flow?

In thermal equilibrium no current can flow if one connects the two sides of the junction using a perfectly conducting wire.

The built-in potential existing at the junction will remain the same, drift and diffusion currents will cancel in the depletion region. At the junctions between the wire and the p and n sides something similar happens: there is a built-in potential, and a depletion region in which drift and diffusion currents cancel out. In thermal equilibrium the sum of the three built-in potentials is zero:

$$ V_{\mathrm{metal}/p} + V_{p/n} + V_{n/\mathrm{metal}} = 0 $$

so no net current can flow around the entire circuits. Drift and diffusion currents exist at the junctions but locally cancel each other out. In the equation above $V_{p/n} \equiv V_{0}$, where $V_{0}$ is the notation for the built-in potential used in the question.

2) An external bias $|V|$ < $V_{0}$ is applied ...

When a bias voltage is applied, it appears (almost entirely) across the depletion region in the pn junction. This happens because the resistance of the depletion region is very large compared to the resistance of the undepleted p and n regions, and also very large compared to the resistance of the depletion region at the metal-semiconductor contacts.

The reason for this is that at the depletion region of the pn junction there is a significantly lower number of mobile carriers than everywhere else in the system. We are assuming here that the contacts between the voltage source and the p and n sides are ohmic contacts, such that they will have a very narrow depletion region and therefore negligible resistance.

The built-in potentials of the metal-semiconductor junctions stay the same (they have no resistance), and the built-in potential of the pn junction is modified by the applied voltage:

$$ V_{p/n}^{\mathrm{bias}} = V_{p/n} + V $$

We then have across the entire system:

$$ V_{\mathrm{metal}/p} + V_{p/n}^{\mathrm{bias}} + V_{n/\mathrm{metal}} = V $$

Current-Voltage curve for the pn junction

The current across the system for a given bias voltage $V$ is given by

$$ I = I_{s}( e^{qV/kT} - 1 ) $$

where $I_{s}$ is the reverse saturation current. The fact that this curve is not linear in $V$ means that one cannot really define a resistance for the pn junction. I hope this helps clarify the last part of your second point.

Answer 3

Background (Taken from Millman's book)

An ideal p-n diode has zero ohmic voltage drop across the body of the crystal. We assume that the external bias voltage appears directly across the junction.To justify this assumption we must specify how electric contact is made to the semiconductor from the external bias circuit.we indicate metal contacts with which the homogeneous p-type and n-type materials are provided. We thus see that we have introduced two metal-semiconductor junctions, one at each end of the diode. We naturally expect a contact potential to develop across these additional junctions. However, we shall assume that the metal-semiconductor contacts have been manufactured in such a way that they are nonrectifying. In other words, the contact potential across these junctions is constant, independent of the direction and magnitude of the current. A contact of this type is referred to as an ohmic contact.We are now in a position to justify our assumption that the entire applied voltage appears as a change in the height of the potential barrier. Inasmuch as the voltage across the metal-semiconductor ohmic contacts remains constant and the voltage drop across the bulk of the crystal is neglected, approximately the entire applied voltage will indeed appear as a change in the height of the potential barrier at the p-n junction.

Now let's consider the problems you mentioned.

1) If the n and p doped regions are externally connected using a perfectly conducting wire, why will not any current flow?
if we short-circuit p-n Junction Under these conditions, as we show below, no current can flow($I=0$) and the electrostatic potential $ \Delta V$ remains unchanged and equal to the value under open-circuit conditions. If there were a current ($I \neq 0$), the metal would become heated. Since there is no external source of energy available, the energy required to heat the metal wire would have to be supplied by the p-n bar. The semiconductor bar therefore, would have to cool off. Clearly, under thermal equilibrium the simultaneous heating of the metal and cooling of the bar is impossible, and we conclude that $I=0$ Since under short-circuit conditions the sum of the voltages around the closed loop must be zero, the junction potential $\Delta V$ must be exactly compensated by the metal-semiconductor contact potentials at the ohmic contacts. Since the current is zero, the wire can be cut without changing the situation, and the voltage drop across the cut must remain zero. If in an attempt to measure $ \Delta V$ we connected a voltmeter across the cut, the voltmeter would read zero voltage. In other words, it is not possible to measure contact difference of potential directly with a voltmeter.

2) what will be the potential drops which would sum to zero in this case? Will drop due to the resistance of semiconductor play a par in it? If yes, then there cannot be any ideal resistance-less semiconductor junction, can there?

An ideal semiconductor diode is just a model called "zeroth order model" also reffered to as the ideal diode model
. It is the most rough approximation used in the Large-signal Model of a diode. This model is used when the resistance connected in series with diode is very large than diode's resistance.
Neither an ideal diode nor an ideal conductor exists in reallity ,these are just mathematical models of physically reliable lumped circuits.

NOTE: For the analysis of P-n junction we usually assume that whole of the applied voltage appears directly across the deplition region i.e we neglects the crystal resistance of remaining body of diode but we do not neglect the resistance of deplition region.

Assuming connecting wires are perfectly conducting it should be clear that $\Delta V$ is numericaly equal in magnitude to the constant m-s junction potential and resistance of m-s junction is assumed to be 0. So if the voltage applied across the diode(containing m-s junction) is $|V|$ . This particular $|V|$ will appear across the junction.
Let V is the applied voltage either +ve or -ve. Since deplition region has some finite resistance so it will have certain electron mobility $\mu_n$ and hole mobility $\mu_p$.
The net hole current density $J_p$ is sum of drift and diffusion current components i.e
$$J_p= qp\mu_p E -qD_p \frac{dp}{dx}$$
Since $J_p$ is small we can compute $E$ created by $V$ easily.
$$qp\mu_p E=qD_p \frac{dp}{dx}$$
$p$ is a function of applied voltage $V$ . For an ideal diode these equations are irrelevant as $\mu_p$ will be $\infty$ and $0%$ amount of $V$ will appear across deplition region.