A speed limit for static friction?

Question

Suppose that a box is sliding along the floor, subject to kinetic friction and a pushing force (in the direction of its motion) that is slowly decreasing. The box is decelerating, and eventually the box is moving forward at an extremely tiny and decreasing speed.

My questions are:

1. Does the box ever reach a sufficiently tiny speed that the friction becomes more like static than kinetic friction, even though the box is actually moving, albeit very slowly?
2. At what speed does this occur?
3. What is the transition like? Does the frictional force change from kinetic to static friction linearly as a function of speed?
4. My intuition suggests that the answer to question (3) is no given sufficient resolution; supposing this is true, is there some interesting substructure to the friction-versus-speed graph that might actually betray some sort of information about the molecular structure (averaged out over the surface area) of the materials?

Answer 1

Have a look at How is frictional force dependent on normal reaction? where I explain how the frictional force arises from interactions between molecules at the sliding surfaces.

The reason that kinetic friction is different from static friction is that when the surfaces are sliding energy is being continuously added to the molecules at the surfaces. This energy will cause vibrational excitations of the molecules, which is what heat is, and that's why the sliding surfaces get hot when there is friction.

There will be some characteristic relaxation time for the molecules at the surface, which is basically the time taken for those molecules to dissipate their vibrational energy into the bulk of the material. In fast sliding energy is being added to the surface molecules faster than it can be dissipated, so the molecules stay "hot" and friction is reduced.

However as the relative speed decreases there will eventually come a point where the surface molecules can "cool" faster than energy is being added to them, and this is the point where the sliding abruptly stops and the friction transitions from kinetic to static.

Friction is a complicated process, and the above is an oversimplification but hopefully an oversimplification that helps give you the basic idea. In real life it's impossible to predict the point at which static friction takes over. A friend of mine tried to model this for a simplified surface using a Monte Carlo technique as part of is PhD, but to make the calculations possible the system had to be so simplified that it was difficult to relate it to any real system.

Answer 2

The model used for friction in elementary Newtonian mechanics courses is actually like this (image source):

although often it is even further simplified by assuming that the kinetic friction has value of the maximum static friction, that is $$\mu_k=\mu_s$$.

So, within this simple mechanical model, logically, as long as the box is moving the kinetic friction has constant value. Only after the box stops ($v=0$) could the value of friction force decrease.

The problem with reasoning about tiny speeds is that it leads to Achilles and the tortoise paradox, which is actually a paradox only because we are sticking to a model that is too crude to describe this regime/ we try to reason in terms of continuous speed while the friction is due to the random irregularities of the surface that have finite size: one bump being a bit bigger may abruptly stop the object ("abruptly" on the scale of the "tiny speed). For an observer with realistic error of measuring speed and position (which allow applying simple mechanical models) the things look continuous.

In essence, I concord with point $4$ of the Q:

4. My intuition suggests that the answer to question (3) is no given sufficient resolution; supposing this is true, is there some interesting substructure to the friction-versus-speed graph that might actually betray some sort of information about the molecular structure (averaged out over the surface area) of the materials?

Interestingly, the actual coefficient of friction is indeed speed-dependent, but this is a dependence that is too material-specific, to be described by a generic passe-partout model, as those use din elementary mechanics. Here is an example:

From my brief search in google, the issue is of non-negligeable importance in some areas, as, e.g., scanning electron microscopy - where the microscope tip is literally dragged along the sample surface.

Related: How does friction depend on velocity?

Answer 3

Does the box ever reach a sufficiently tiny speed that the friction becomes more like static than kinetic friction, even though the box is actually moving, albeit very slowly?

The simple model of kinetic friction and static friction assumes a discontinuous transition from one frictional force at non-zero relative speed to a different force at zero relative speed. Since such a discontinuous transition is unphysical, then there must in reality be some range of speeds in which the frictional force smoothly changes from one value to the other.

At what speed does this occur?

What is the transition like? Does the frictional force change from kinetic to static friction linearly as a function of speed?

This will depend on the materials involved and the extent of lubrication between them. All models for the transition region between kinetic and static friction are empirical and you can only determine an appropriate model and its parameters by performing experiments.

How is the transition from kinetic to static friction modeled? and https://en.wikipedia.org/wiki/Stribeck_curve may be relevant.

Answer 4

Your questions, and the answers you have recently received along with the links referenced therein, illustrates that there appears to be no universally acceptable explanation of what causes “friction”, or even if we can ascribe a single term to explain certain observable phenomena. But I think we may be able to agree on some answers to your questions, which I will address after I first present the following for deliberation.

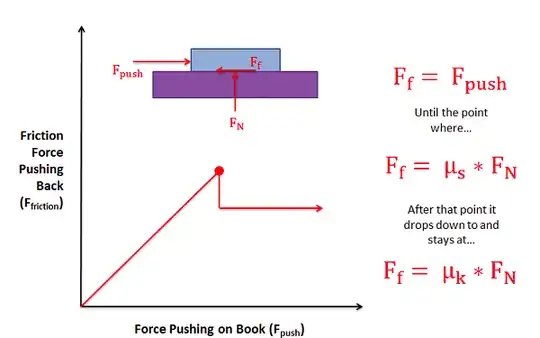
We observe certain phenomena associated with the relative motion between two surfaces. First we observe it appears to require a certain minimum amount of force to initiate relative motion, that is, to initiate "sliding". Second we observe that once relative motion is underway, there appears to be a force that acts in opposition to that relative motion, or sliding. We use the term "static friction" to describe the first observation and "kinetic (or dynamic, or sliding) friction" to describe the second observation. We assign certain "friction coefficients" to each term based on testing different combinations of materials along with the conditions associated with the surfaces (roughness, presence of lubricants, etc. ).

Based on tests and resulting calculated “friction coefficients” we attempt to develop a model for what friction is that can predict the observed phenomena. Probably the most common, albeit simplistic one, is the so called “Standard Model” of friction. One description of this model and the assumptions upon which it is based can be found here: http://hyperphysics.phy-astr.gsu.edu/hbase/frict.html.

While this model does a reasonable job in many situations, it doesn’t take long before we encounter exceptions to it and to the assumptions upon which it is based. For example, while lesser surface roughness is generally associated with lower friction because of the theoretical lesser degree of interlocking between microscopic irregularities at the surface, we find the counter intuitive observation that the coefficient of static friction between very smooth, clean and dry aluminum surfaces is among the highest encountered (re: https://www.engineeringtoolbox.com/friction-coefficients-d_778.html). This forces us to acknowledge the different phenomenon of increased electrostatic attraction between the molecules at the surfaces due to closer contact. It also makes us question whether any single model or combination of models can possibly satisfy all our observations.

That said, let’s see if we can agree on some basic things associated with the terms static and kinetic friction that we can apply to your specific questions (1) through (4).

The first is to agree to define the static friction force as that which resists the initiation of relative motion between contacting surfaces, whilst we agree to define the kinetic friction force as that which acts in opposition to relative motion already underway.

1. Does the box ever reach a sufficiently tiny speed that the friction becomes more like static than kinetic friction, even though the box is actually moving, albeit very slowly?

If we agree the static friction force only exists where there is no relative motion and agree the kinetic friction force only exists where relative motion is underway, then as long as the box is moving friction is kinetic and as long as the box is not moving friction, if any, must be static. There is no in-between.

I emphasize “if any” regarding static friction because if the applied force is reduced to zero, there will be no static or kinetic friction once it stops. If the applied force is not reduced to zero, when the box stops there will be a static friction force equal and opposite to the applied force. Keep in mind that the applied force at that point will always be less than the maximum possible static friction force, based on the friction plot in the Hyperphysics link.

2. At what speed does this occur?

Based on the answer to (1), the answer to this and to the title to your post, “A speed limit for static friction?” would appear to be zero for friction to become static.

3. What is the transition like? Does the frictional force change from kinetic to static friction linearly as a function of speed?

If we agree the friction must be static or kinetic, without an “in between”, then the transition from kinetic to static would have to be, for want of a better term, abrupt, in the same way that the transition from static to kinetic friction in response to a gradually increasing applied force before sliding begins is abrupt as shown in the friction plot.

The chief difference is the abrupt transition from static to kinetic friction involves a sudden decrease in the friction force, shown as a straight vertical line on the friction plot for the Standard Model, whereas the transition from kinetic to static friction would theoretically not involve a change in the magnitude of the friction force when it changes from kinetic to static. This seems to align with my own real life observations.

If I try to initiate motion of a box on the floor by gradually increasing my pushing force I observe that when the box "breaks free" from the floor and starts to move, the resistance to my pushing force seems to suddenly and significantly decrease. On the other hand, for the box to stop it seems I have to reduce my pushing force to the point where it feels like I am exerting almost no force at all. Certainly much less force than I needed to initiate motion in the first place.

4. My intuition suggests that the answer to question (3) is no given sufficient resolution; supposing this is true, is there some interesting substructure to the friction-versus-speed graph that might actually betray some sort of information about the molecular structure (averaged out over the surface area) of the materials?

Based on my response to (3), I would agree with your “no” answer. The “reason” at the molecular level would appear to depend on the specific combination of materials and conditions that prevail at their surfaces. As already acknowledged, there is no simple single answer that can apply.

Hope this helps.