Mathematically viewing, the Aharonov-Bohm experiment shows that the magnetic field creates a connection with a nonzero holonomy on a multiply-connected domain. This means that there isn't a state function that is continuous on that domain. This isn't a problem if we regard the state function as an element of $L^2$, since the elements of $L^2$ need not be continuous, only square-integrable. But the state function must be unambiguous up to a phase factor, and this is my problem. If we omit continuity on a zero-measure subset, then picking two different zero-measure subsets, the functions belonging to them will not differ by a constant phase factor.
A bit more details
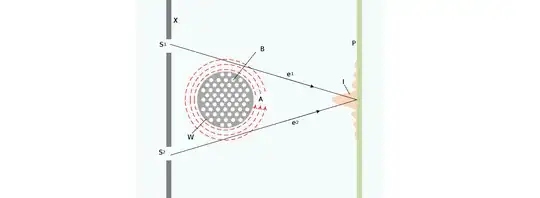
The experimental setting described in this Wikipedia article looks like this:
The configuration space of the electron is the physical space minus the space occupied by solid objects like the wall (containing the slits) and the solenoid. The states of the electron are square-integrable functions on this multiply-connected domain. In the case when there is no current in the wire of the solenoid, let this state function be $\psi_0$, and let this state be $\psi_A$ when we switch the current on. Choosing a circle $c$ around the solenoid, let the restriction of $\psi_0$ to $c$ be $\psi_{0,c}$ and the restriction of $\psi_A$ to $c$ be $\psi_{A,c}$. Let's define $\Delta\psi:= \psi_{A,c}/\psi_{0,c}$.
Let's pick a point $p$ on the circle and take a parametrization $\gamma_p:[0,1]\to c: \lambda\mapsto \gamma_p(\lambda)$ of $c$ so that $\gamma(0)=\gamma(1)=p$. Then, according to the quantum theory of the A-B effect, $$\lim_{\lambda\to 1} \Delta\psi\circ\gamma(\lambda)=\Delta\psi\circ\gamma(0)e^{i\frac{q}{\hbar c}\oint_c A}\tag 1$$
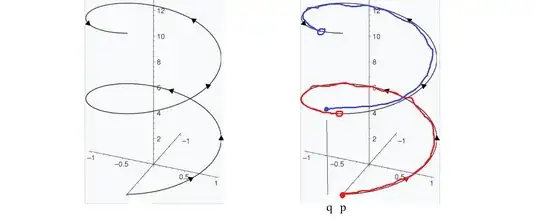
Since $\gamma(0)=\gamma(1)=p$, $\Delta\psi\circ\gamma(1)=\Delta\psi\circ\gamma(0)=\Delta\psi(p)$, so $\Delta\psi$ isn't continuous at $p$,$\!\phantom{|}^{[*]}$ except when $\frac{q}{\hbar c}\oint_c A=2n\pi\ (n\in\mathbb N)$. This condition should imply the quantizedness of the flux in the solenoid, but in the Aharonov-Bohm effect, flux isn't quantized. In the discountinuous case, picking another point $q$ on $c$, we get a function that isn't continuous at $q$. It's not a problem that choosing different points on $c$ we get different state functions, but if these functions represent the same quantum state, then they should differ only by a complex number of modulus 1 as factor. But this is not the case, as seen in the following illustration (from $q$ to $p$, the factor is $1$ while on the rest, the factor is different from $1$).
What is the resolution of this problem?
Edit
I am increasingly inclined to think that the above contradiction cannot be resolved within the framework of standard quantum mechanics. Is there a widely accepted alternative mathematical model of quantum mechanics that can describe exactly the Aharonov-Bohm experiment?
Perhaps the bundle formalism of quantum mechanics
Or the Segal quantization?
Or the Coherent foundations?
Edit 2
It seems that the problem is that the configuration space $Q$ of this quantum mechanical system is multiple-connected and standard quantum mechanics using the Hilbert space of states $L^2(Q)$ works only on simply connected $Q$. A solution could be to take a subspace of $L^2(\tilde Q)$ instead, where $\tilde Q$ is a $U(1)$ bundle on $Q$ (see Balachandran et al, Classical Topology and Quantum States), or the universal cover of $Q$. But I don't see the solution clearly yet.
Footnote
$\!\phantom{|}^{[*]}$ This property is seemingly similar to the case of the action of the Galilean group on the projective Hilbert space $P(H)$, where there isn't a continuous lift to the Hilbert space $H$ (regarded as an $U(1)$-bundle on $P(H)$. But here, $\psi$ is a function on the base space, not a section of a $U(1)$-bundle. The phase of $\psi$ is definite in each point. The phase freedom is to multiply the whole $\psi$ with a complex number of modulus 1, not to multiply its values point-by-point. The usual heuristic workaround of this problem is that we say that the particle is dragged along some pathes and meantime, it "picks a phase". But the notion of "dragging a particle" is alien to quantum machanics. In this case, where is the state function in a given time instance? I think, a more clear approximation would be to handle the $x$ coordinate of the particle classically, as Beltrametti and Cassinelli does in the case of the double slit experiment and to use wave functions defined on the planes perpendicular to the $x$-axis (see here). Or the other possibility, to make a kind of quantum mechanics in which the values of the state functions aren't complex numbers, but fibers of a $U(1)$-bundle. Of course, there is the Feynman path integral formalism, but currently I'm looking for a solution inside standard quantum mechanics, or at least, which is more close to the standard quantum mechanics than the path integrals.