How to solve bound states of 2D finite rectangular square well?

Question

I want to solve bound states (in fact only base state is needed) of time-independent Schrodinger equation with a 2D finite rectangular square well \begin{equation}V(x,y)=\cases{0,&$ |x|\le a \text{ and } |y|\le b$ \\ V_0,&\text{otherwise}}.\tag{1}\end{equation} $$\Big[-\frac{\hbar^2}{2m}(\partial_x^2+\partial_y^2)+V(x,y)\Big]\psi(x,y)=E\psi(x,y)$$ At first glance, this problem is simple. It seems that the solution is variable-separable and can be written as $\psi(x,y)=f(x)g(y)$. Then $$ \frac{f''(x)}{f(x)}+\frac{g''(y)}{g(y)}+\frac{2m}{\hbar^2}(E-V)=0.$$ Let $E=E_x+E_y$ and $V=V_x+V_y$, then the problem is reduced to two 1D problems $$\cases{f''(x)+\frac{2m}{\hbar^2}(E_x-V_x)f(x)=0\\g''(y)+\frac{2m}{\hbar^2}(E_y-V_y)g(y)=0}.$$

However, how to determine $V_x$ and $V_y$ in the 2D space? A definitely wrong method is making $$ V_x=\cases{0,&$|x|\le a$\\V_1,&$|x|>a$}\text{ and }V_y=\cases{0,&$|y|\le b$\\V_2,&$|y|>b$}\tag{2}.$$ In fact, the potential Eq. (2) is equivalent to two independent "1D finite square well" problems in $x$ and $y$ direction respectively. However, a careful reader will note that the potential Eq(2) is DIFFERENT from Eq(1), which means that the potential Eq(2) is NOT what we want. It's not a rectangular well, but as following .

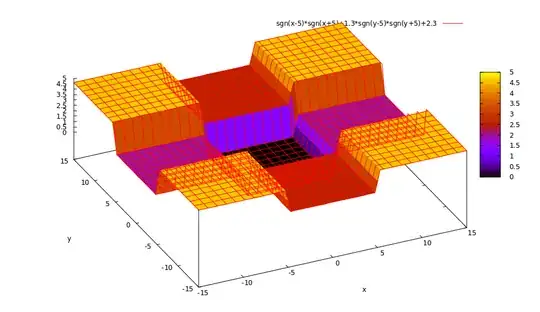Then, I find that a variable-separable bound state for finite 2D square well does not exist. Although analytical solutions exist in each region with a constant potential, problems occur when matching boundary conditions to keep the continuity of $\psi(x,y)$. Unlike matching boundary condition at descrete points in 1D, in 2D we have to match boundary conditions along lines, e.g., $$ f_1(a)g_1(y)=f_2(a)g_2(y)$$ in the boundary between $x<a$(region 1) and $x>a$ (region 2). This leads to $$ g_1(y)/g_2(y)=f_2(a)/f_1(a)=constant.$$ Matching all boundaries this way will lead to that $\psi(x,y)$ have to be 0 outside the well. But this cronsponds to the case of INFINITE well. It's not the solution of finite well. Then I think no solutions exist under the separating-variable method.

Then, the question is, beyond separating-variable method, how to solve this problem?

BTW: Does anyone know that what kind (shape) of 2D well is solvable for bound states and how? (Potential with circular symmetry is excluded, because I know how to solve it. I want to find another shape of 2D well which is solvable.)

Answer 1

This 2D Problem is Solvable, I knew because I have solved a similar 2D problem involving an electron trapped in a 2D potential circle - it has also been detected by IBM scientist in their Lab prior.

There will be two approaches here, one would be the penetrable barrier and the non-penetrable barrier. Since the problem did not mention the transmission function, it is safe to assume that this problem is non-penetrable.

With regards to your problem, its pretty solvable by Separation of Variables, you have just missed some important steps, I will give you a start-up so that you can proceed with the Technique. This problem has two regions, don't try to mix them cause you will get stuck as you are now. The two regions are simply IN-box and OUT-box.

CASE 1: IN-box

At $|x| \leq a$ and $|y| \leq b$; $V(x,y)=0$

that means your box has '$a$' length on $ \pm x$-axis, thats $2a$ overall, same as to with $y$. And in that region, any particle or wave experiences a zero potential, that is $V(x,y)=0$ as your problem says, so your DE will reduce to:

$$-\frac{\hbar^2}{2m}(\partial_x^2+\partial_y^2)\psi (x,y) -E \psi (x,y) = 0$$

by this you can then employ separation of variables. Remember that your $E(x,y)=E$ is the a base energy (as you wish to solve) then it should therefore be the same anywhere inside, at its base state. Thus it is a constant and does not have any $x$ or $y$ component, no breaking or sum involved, you treat it the same as you treat a constant under the Technique of Separation.

CASE 2: OUT-box

If otherwise a particle or wave falls outside $a$, that is $|x| > a$, then it will experience a potential $V_0$, so your potential $V(x,y)$ becomes $V_0$ as the condition of your problem says, same goes with $y$-axis. Well $V_0$, as the name itself is a constant, it does not depend on either $x$ or $y$, so NO need separations for $V_0$, your DE would then be

$$-\frac{\hbar^2}{2m}(\partial_x^2+\partial_y^2)\psi (x,y) +(V_0-E)\psi (x,y) = 0$$

again, this is also a separable equation, then therefore your Problem is Solvable.

So overall, there will be two sets of solutions to the problem: one for IN-Box and one for OUT-box.

BTW: You seem to have problem with separations involving constants, kindly review it. I wish to discuss it, but that is not Physics anymore.

Answer 2

I think this problem is similar to the problem of finding modes of rectangular dielectric waveguide. In this case, you can use the effective-index method for finding the approximated solution (For your problem, we can call it effective-potential method). For more information about effective-index method see the following articles:

• Effective-index analysis of optical waveguides: Link

• Analysis of integrated optical waveguides: variational method and effective-index method with built-in perturbation correction: Link

The basis of this method is that the mode of a waveguide can be separated into products of two functions, one in $x$ direction which is dependent only on $x$ and one in $y$ direction which is dependent only on $y$. These can be solved independently and combined to produce the mode structure. In this way, the 2D waveguide structure can be separated into two single structures, one being a step index planar waveguide in $x$ direction and other in $y$ direction. In fact, this is same as your suggestion for introducing $V_x$ and $V_y$, but in a special way that the solution is very closed to the exact solution

Answer 3

So far, the only thing that I can be sure of is that there is no solution of the form $\psi(x,y)=g(y)f(x)$, which would lead to an obvious contradiction:

If we have a solution $\psi(x,y)==f(x)g(y)$, denote $\frac{f''}{f}=F(x),\frac{g''}{g}=G(y)$, For any fixed x<-a, F(x)+G(y)=constant requires G(y) is constant, similarly, fixed y<-b, requires F(x) is constant, but F(x)+G(y) is not constant in the whole x-y plane , thus =><=.

Answer 4

The problem has, indeed, no closed form solution. One elementary way of seeing this is the following: if there were a solution, it could be applied equally well to a repulsive hard suqare potential. The formula obtained for this repulsive hard square potential could then be considered in the limit of an infinitely repulsive hard square. This would mean that scattering off a square obstacle could be solved. This is notoriously not the case, because a square contains 4 angles on which the wave is diffracted, and diffraction on one single angle is extremely hard.

Answer 5

Well, if I'm right, then this problem has no solution - at least no finite analytical one. And btw. the problem is more general than one might think. Look at the upper right quadrant ($x\gt0$ and $y\gt0$). Then the boundary conditions are symmetry boundary conditions (scalar product of normal vector and gradient of the solution is zero at $x=0$ and $y=0$). Furthermore, at x=a and x=b, the solution must be continuous (and the gradient, too, but this is not important). And, of course, the solution must vanish at infinity. These boundaries actually generate four regions: 0 - ($0\lt x \lt a, 0\lt y\lt b$), 1 - ($0\lt x\lt a, y\gt b$), 2 - ($x\gt a, 0\lt y\lt b$), and 3 - ($x\gt a, y\gt b$). In each of these regions, the solution is separable, as you correctly mentioned. The Schrodinger equation now makes the general statement. The total curvature in each region is a sum of two curvatures along the respective cartesian directon. $B_i^2=B_{i,x}^2+B_{i,y}^2$ with $i=0,1,2,3$. So, you have four equations for eight curvatures. Another four equations are added if you use the continuity boundary conditions. Namely, along the boundaries, the parallel curvatures at the adjacent regions must be equal. For instance, between region 0 and 1, $B_{0,x}^2=B_{1,x}^2$, etc. This, in total gives you a linear equation with a 8 by 8 square matrix, and a right-hand side (RHS) vector containing only the total curvatures $B_i^2$. First of all, this matrix is exactly singular (i.e. it does not have the full rank). To have any non-trivial solution at all, you have to make the RHS of the same rank. This gives you a condition for the total curvatures (which are related to the potential and the eigenvalue). And this condition is that the curvatures must be the same. Essentally, this means that the potential is everywhere zero - a clear contradiction to what we wanted. Please try this approach and report me your findings, as I might be wrong, as I outlined at the beginning ;)